preface
何恺明的《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition》提出了 spp 空间金字塔池化层,解决了传统的卷积神经网络需要固定输入图片的尺寸这一问题。因为传统的卷积神经网络有全连接层,如果输入的图像尺寸不一致的话,全连接层神经元的个数也要进行相应的修改,所以无法完成训练,而对于卷积层来说没有这个限制。
之前的做法是在训练之前将数据集给 resize 到网络能够接受的固定尺寸(例如 224 x 224),然后再训练。用了 spp 之后就不需要进行这一步骤了,反正只要让最终的全连接层的 input 相等就行了,那就在卷积层和全连接层之间加入一层网络,使得不论最终卷积层得到了多大的 feather map ,都输出相同的 vector 送入全连接层,这就是 spp 做的事。

那么 spp 是怎么做到不论输入多大的 feather map 输出都相同的呢?挺有意思的,下面是论文中给出的原理图,第一遍看我还没看懂,看了别人的博客才知道是什么意思。
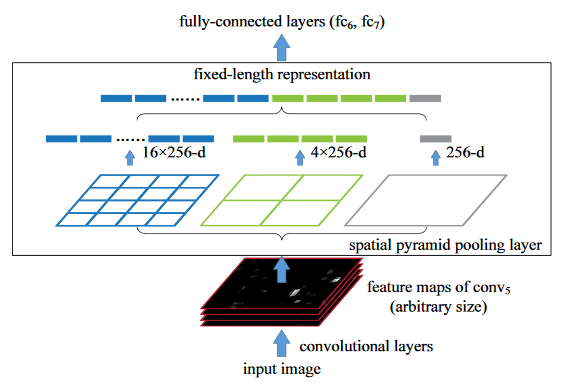
In each spatial bin, we pool the responses of each filter ( throughout this paper we use max pooling).The outputs of the spatial pyramid pooling are kM-dimensional vectors with the number of bins denoted as M (k is the number of filters in the last convolutional layer). The fixed-dimensional vectors are the input to the fully-connected layer.
上面是论文中的解释,用我的话来理解就是,我们只要人为设定好 spp layer 需要的 spatial bin 就好了,这里 spp 接受来自最后一层卷积层的 feather map,然后用了 3 个池化窗口,其中的 bin 的个数分别是 16、4、1。也就是说这些 feather map 最终经过 这三个池化窗口 size 会变成 (4,4)、(2,2)、(1,1),用人话说也就是二维平面上最后会是 21 个像素,然后别忘了 feather map 还有 256 个通道的,将这些特征全部展开成一维向量后送入全连接层,最终输出到全连接层也即是 (16+4+1)x256 个向量。所以,只需要人为设定好 spatial bin 的个数就能够产生固定长度的输出。
下面是 spp 的代码实现,也就是怎样将一个随机的 feather map 变成固定长度的输出 (代码运行有问题,但是思路是没错的)
import math
def spatial_pyramid_pool(self,previous_conv, num_sample, previous_conv_size, out_pool_size):
'''
previous_conv: a tensor vector of previous convolution layer
num_sample: an int number of image in the batch
previous_conv_size: an int vector [height, width] of the matrix features size of previous convolution layer
out_pool_size: a int vector of expected output size of max pooling layer
returns: a tensor vector with shape [1 x n] is the concentration of multi-level pooling
'''
'''上图中 out_pool_size 为 [4, 2, 1]'''
for i in range(len(out_pool_size)):
'''math.ceil 向上取整'''
h_wid = int(math.ceil(previous_conv_size[0] / out_pool_size[i]))
w_wid = int(math.ceil(previous_conv_size[1] / out_pool_size[i]))
'''要加1,因为此处单位是像素'''
h_pad = (h_wid*out_pool_size[i] - previous_conv_size[0] + 1)/2
w_pad = (w_wid*out_pool_size[i] - previous_conv_size[1] + 1)/2
'''MaxPool2d(kernel_size, stride=None, padding=0)'''
maxpool = nn.MaxPool2d((h_wid, w_wid), stride=(h_wid, w_wid), padding=(h_pad, w_pad))
x = maxpool(previous_conv)
if(i == 0):
'''展开成向量,num_sample是batch_size'''
spp = x.view(num_sample,-1)
else:
'''拼接成 vector'''
spp = torch.cat((spp,x.view(num_sample,-1)), 1)
return spp
在 forward 前向传播的时候就不用再去管输入是多少了,只要确定好 spp 的参数就行了
class SPP_NET(nn.Module):
'''
A CNN model which adds spp layer so that we can input multi-size tensor
'''
def __init__(self, ndf=64):
super(SPP_NET, self).__init__()
'''省略一堆不重要的东西……'''
self.output_num = [4,2,1]
self.conv5 = nn.Conv2d(ndf * 8, 64, 4, 1, 0, bias=False)
self.fc1 = nn.Linear(10752,4096)
self.fc2 = nn.Linear(4096,1000)
def forward(self,x):
'''省略一堆……'''
x = self.conv5(x)
spp = spatial_pyramid_pool(x,1,[int(x.size(2)),int(x.size(3))],self.output_num)
fc1 = self.fc1(spp)
fc2 = self.fc2(fc1)
s = nn.Sigmoid()
output = s(fc2)
return output
在上面的代码中,由 conv5 产生 feather map,然后经过一个 spp,这个 spp 层有三个 pooling 窗口,最终得到一个 10752 维的特征向量,这个数字不会随着 input 图像的 size 而发生改变,只和最后一层卷积的 channels 和 spp 的 bin 也就是上面的 output_num 有关。我们来算一下,conv5 的输出 channel 为 64*8 = 512 ,output_num 是 [4, 2, 1],因此二维平面有 4*4 + 2*2 + 1*1 = 21 个像素,最终的输出就是 512*21 = 10752 ,跟网络输入尺寸无关!
reference
https://arxiv.org/abs/1406.4729
https://github.com/yueruchen/sppnet-pytorch