LeetCode刷题记录

1 两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9 所以返回 [0, 1]

我只会用暴力解法，看了题解才知道哈希表可以这样用，屌！就，用一个表存入数据和索引，遍历这个表一次，如果 target 减去当前元素的值在哈希表里面的话可以直接返回索引，就不需要双重循环遍历了。更牛逼的做法是变将数据和索引存入哈希表边检查有没有存在，有的话可以不用将剩下的数据存完就返回了。

class Solution {	// 我写的辣鸡暴力法
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> result;
        for (int i = 0; i < nums.size(); ++i) {
            int t1 = nums[i];
            for (int j = i + 1; j < nums.size(); ++j) {
                int t2 = nums[j];
                if (t1 + t2 == target) {
                    result.push_back(i);
                    result.push_back(j);
                }
            }
        }
        return result;
    }
};

这就是更牛逼的做法，不过 C++ 的 map 中的 find 和 count 方法针对的都是 key ，并不是 value，因此如果我们想要知道索引号的话就得将索引和数据反过来存进 map 中

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        map<int,int> a;//提供一对一的hash
        vector<int> b(2,-1);//用来承载结果，初始化一个大小为2，值为-1的容器b
        for(int i=0;i<nums.size();i++)
        {
            if(a.count(target-nums[i])>0)   //找到了目标
            {
                b[0]=a[target-nums[i]];
                b[1]=i;
                break;
            }
            a[nums[i]]=i;//反过来放入map中，用来获取结果下标
        }
        return b;
    };
};

20 有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例 1:

输入: “()” 输出: true

示例 2:

输入: “()[]{“ 输出: false

遇到这种配对的问题，首先应该想到的就是用栈来做，如果第一个字符就是右闭合的括号的话，直接返回 False，否则遇到左括号就将其压栈，遇到右括号就将其和栈顶元素比较是否能够闭合，能的话就将栈顶元素弹出来，不能的话就返回 False。最后遍历完字符串之后，如果栈空了说明全部都配对了，否则返回 False

演示图

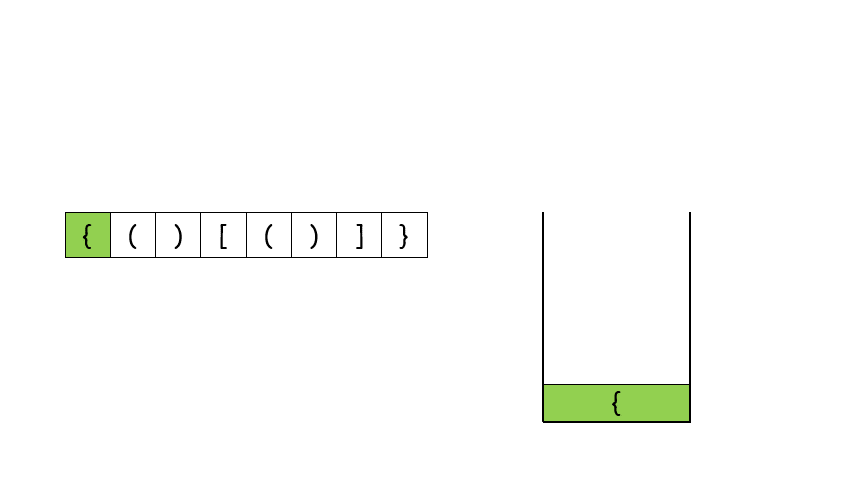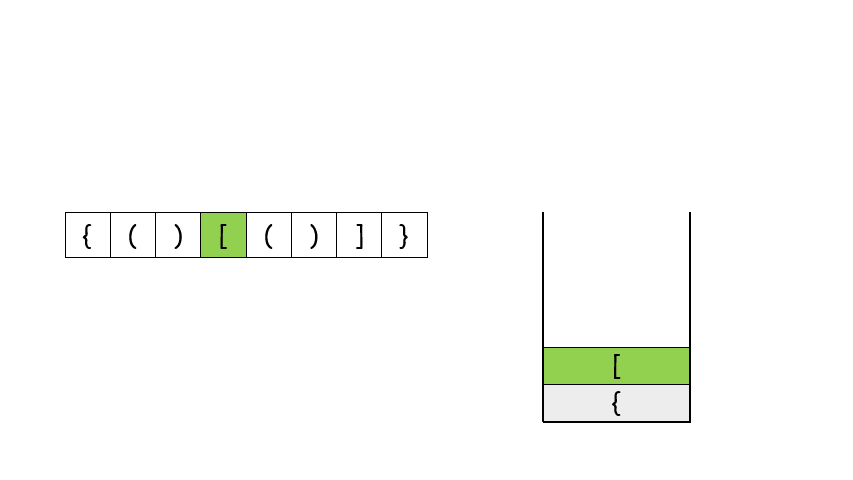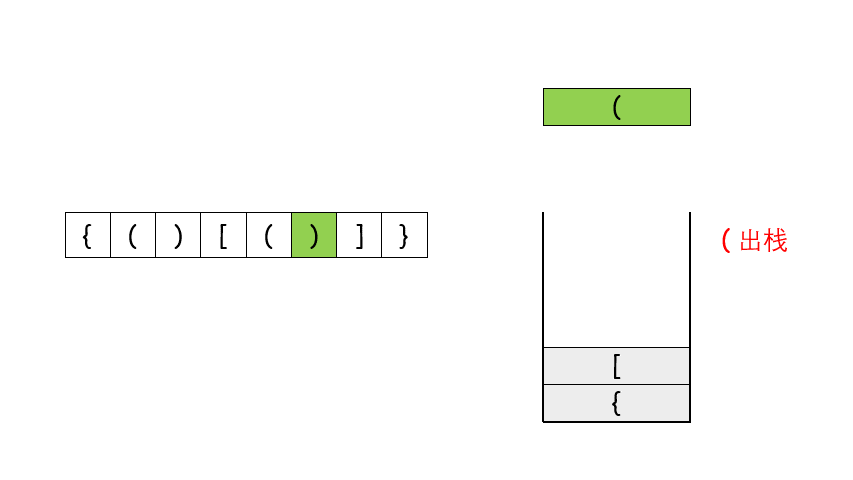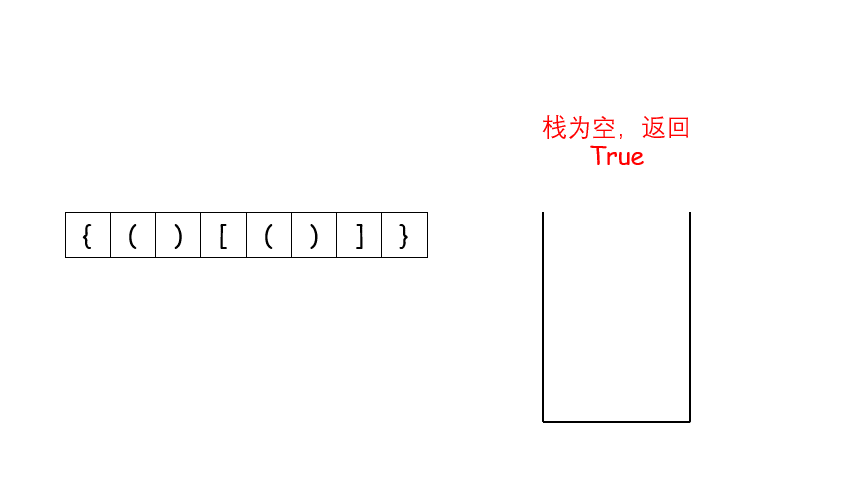
class Solution {
public:
    bool isValid(string s) {
        /*
1. 首先设定哈希表,依次保存三个开括号`(分别对应1,2,3)`与三个闭括号`(分别对应4,5,6)`,以及栈`(只放入开括号,遇到对应闭括号,则出栈)`还有最后一个正确bool值,判断是否正确`(比如第一个就是闭括号,必然错误)`,且默认为真
2. for遍历string字符串
   1. 如果为开括号,入栈
   2. 否则栈非空时,且接下来的为对应闭括号,则出栈
   3. 否则(此时隐含表达为'这是个闭括号'),则bool值为假
3. 如果栈非空时,则说明闭括号少了,bool为假
4. 返回bool值
        */
		//哈希表,存储,以及栈
        //傻逼博客不在一起会报错，我只能这样搞，看得懂就行
        data = {'(',1},{'[',2},{'{',3},{')',4},{']',5},{'}',6}
        unordered_map<char,int> m{data};
        stack <char> st;
        //用来判断如果第一个字符就是闭括号怎么办
        bool isTrue =true;
        //遍历string s
        for(char c:s)
        {
        	//如果为开括号,将其入栈
            if(1<=m[c]&&m[c]<=3)st.push(c);
            //如果栈非空,且栈顶元素与接下来的字符(闭括号)相对应,出栈
            //一定要注意栈非空！！！！！！不然会错误
            else if(!st.empty() && m[st.top()]==m[c]-3 )st.pop();
            //否则俩个条件都不满足,意味着一开始就是个闭括号,或者闭括号多了,没有对应开括号在栈里面
            else 
            {
                isTrue=false;
                break;//这里别忘了啊
            }
        }
        //如果for遍历完后,栈非空,意味着开括号多了,则非法
        if(!st.empty()) isTrue=false;
		//返回bool值即可
        return isTrue;
    }
};

136 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1] 输出: 1

示例 2:

输入: [4,1,2,1,2] 输出: 4

这题就很骚，线性复杂度，又不能用额外空间，先来几个正常点的题解。

暴力解法如下，两重 for 循环，找不到配对的数字就返回，找到的话就定义这两个位置为无效，不参与 for 循环

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret, i = 0, j = 0;
        int invalid = INT_MAX;
        for (i = 0; i < nums.size(); ++i) {
            if (nums[i] != invalid){
                for (j = i + 1; j < nums.size(); ++j) {
                    if (nums[j] != invalid && nums[i] == nums[j]){
                        nums[i] = invalid;
                        nums[j] = invalid;
                        break;
                    }                             
                }
                if (j == nums.size()){  // 说明没有找到配对的数字
                    break;
                }
            }
        }
        return nums[i];
    }
};

但是我还是喜欢哈希表的解法，将数字存为 key，次数存为 value，每次有同样的就直接次数 ++ 就行了，我爱哈希表！

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        unordered_map<int, int> ump;
        for (const auto &n : nums){
            ump[n]++;
        }
        int res;
        for (auto it = ump.begin(); it != ump.end(); ++it) {
            if (--(it->second) == 0){
                res = it->first;
                break;
            }
        }
        return res;
    }
};

异或满足分配律和交换律，并且题目说每个数字只出现两次，正好是异或发挥作用的时候，因为一个数异或自己就是 0， 0 和任何一个数异或都是另一个数，这题不断的异或下去就是最终答案（要是说每个数字出现 3 次或者奇数次就不能这么做了）

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res = nums[0];
        for (auto it = nums.begin() + 1; it < nums.end(); ++it) {
            res ^= *it;
        }
        return res;
    }
};

206 反转链表

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL

有两种解法，都是利用双指针来反转，个人觉得第二种解法比较容易些（做链表题一定要在纸上画出来！）

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == NULL)
            return NULL;

        ListNode *cur = NULL, *pre = head;
        while (pre != NULL)
        {
            ListNode *t = pre->next;
            pre->next = cur;
            cur = pre;
            pre = t;
        }
        return cur;
    }
};

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == NULL)
            return NULL;

        ListNode *cur = head;
        while (head->next != NULL)
        {
            // 保护现场，不改变head
            ListNode *t = head->next->next;
            head->next->next = cur;
            cur = head->next;
            head->next = t;
        }
        return cur;
    }
};

209 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的连续子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的连续子数组。

两种方法，首先可以直接用暴力法求解，也就是用两个 for 循环，

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum >= s) {
                    ans = min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

204. 计数质数

统计所有小于非负整数 n 的质数的数量。

示例:

输入: 10 输出: 4 解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

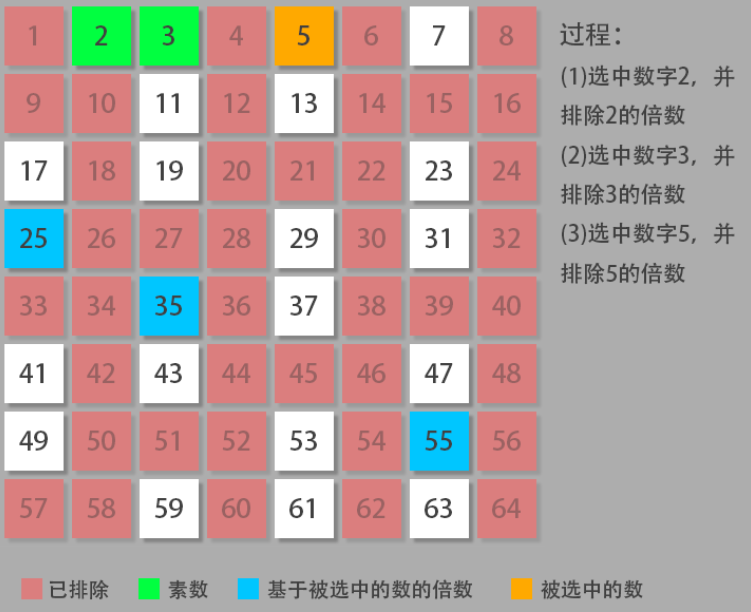
吗的，这题就是计算质数的个数啊，大一 C 语言经典考题，但是我第一遍竟然没写出来……，然后说一下，暴力法不行……会超时，所以可以优化一下暴力法，比如 2 的倍数不可能是质数之类的。当然，还有一种解题思路就是将当前数字的倍数全都除掉，然后最后剩下的就是质数，这个牛逼！

原始暴力法（超时）

class Solution {
public:
    int countPrimes(int n) {
        int res = 1;
        int i = 0, j = 0;

        if (n < 3) {
            return 0;
        }
        for (i = 3; i < n; ++i) {
            int flag = true;
            for (j = 2; j <= std::sqrt(i); ++j) {
                if (i % j == 0) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                res++;
            }
        }
        return res;
    }
};

改进版暴力法（偶数非质数）

class Solution {
public:
    int countPrimes(int n) {
        int res = 1;
        int i = 0, j = 0;

        if (n < 3) {
            return 0;
        }
        for (i = 3; i < n; ++i) {
            if (i % 2 == 0) {
                continue;
            }
            int flag = true;
            for (j = 3; j <= std::sqrt(i); j+=2) {
                if (i % j == 0) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                res++;
            }
        }
        return res;
    }
};

牛逼的方法（厄拉多塞筛法）

sort

class Solution {
public:
    int countPrimes(int n) {
        int res = 0;
        int array[n] = {0};
        for (int i = 2; i < n; ++i) {
            if (array[i] != -1){
                res++;
                // 这句是精髓！
                for (int j = i + i; j < n; j += i) {
                    array[j] = -1;        
                }
            }
        }
        return res;
    }
};

215 数组中的第K个最大元素

二叉树的三种遍历(前序144，中序94，后序145)

451 根据字符出现频率排序

示例 1:

输入: “tree”

输出: “eert”

解释: ‘e’出现两次，’r’和’t’都只出现一次。因此’e’必须出现在’r’和’t’之前。此外，”eetr”也是一个有效的答案。

还是用一个哈希表储存每个字符出现的次数，然后再将表里面的 key 和 value 储存进一个 vector 向量，对其进行排序，然后再输出即可

大佬的题解（unordered_map 内部实现了一个哈希表，是无序的，map 的话内部是实现了一个红黑树，所以里面的数据全都是有序的）

class Solution {
public:
    string frequencySort(string s) {
        unordered_map<char, int> ump;
        for (const auto &c : s) {
            ++ump[c];
        }
        vector<pair<char, int>> vec;
        for (const auto &m : ump) {
            vec.push_back(m);
        }
        sort(vec.begin(), vec.end(), [](const pair<char, int> &p1, const pair<char, int> &p2) { return p1.second > p2.second; });
        string ret;
        for (const auto &v : vec) {
            ret += string(v.second, v.first);
        }
        return ret;
    }
};

我仿照的题解（所以说还是得学一下 stl，大佬这个 for 循环就很实用，不用管迭代器数据是什么类型，直接 auto 一把梭）

class Solution {
    public:
        string frequencySort(string s) {
            map<char, int> mp;
            for (int i = 0; i < s.length(); ++i) {
                mp[s[i]] += 1;
            }
            vector<pair<char, int>> vec;
            for (const auto &m : mp) {
                vec.push_back(m);
            }
            sort(vec.begin(), vec.end(), [](const pair<char, int> &p1, const pair<char, int> &p2) { return p1.second > p2.second; });
            string ret;
            for (int i = 0; i < vec.size(); ++i) {
                ret += string(vec[i].second, vec[i].first);
            }
            return ret;
        }
};

961. 重复 N 次的元素

在大小为 2N 的数组 A 中有 N+1 个不同的元素，其中有一个元素重复了 N 次。

返回重复了 N 次的那个元素。

示例 1：

输入：[1,2,3,3] 输出：3

示例 2：

输入：[2,1,2,5,3,2] 输出：2

我想到了中规中矩的哈希表，存储数字和他出现的次数，边存的时候便检查有没有大于1 ，大于 1 就说明是这个数字

class Solution {
public:
    int repeatedNTimes(vector<int>& A) {
        int res = -1;
        unordered_map<int, int> ump;
        for (auto it = A.begin(); it != A.end(); it++) {
            ump[*it]++;
            if (ump[*it] > 1) {
                res = *it;
            }
        }
        return res;
    }
};

下面一种方法就比较巧妙，直接猜测排列，2N 个元素，如果有两个相同的元素是相邻的，那么直接相邻元素异或为 0 就找到答案了。如果没有两个元素相邻的话，那么前面四个元素的排列一定是 ABAC 或者 ABCA 或者 BABC 这三种，逐一判断一下就知道答案了

class Solution {
public:
    int repeatedNTimes(vector<int>& A) {
        int res = -1;
        for (auto it = A.begin(); it != A.end() - 1;) {
            if(!*it ^ *(it++)) {
                res = *it;
            }
        }
        if (A[0] == A[2] || A[0] == A[3]) {
            res = A[0];
        }
        if (A[1] == A[3]) {
            res = A[1];
        }
        return res;
    }
};