preface
这是在牛客网上根据大家的面经收集过来的题目,并以自己的理解来作出回答,也查阅了很多博客和资料。水平有限,不一定是正确的,欢迎指正,铁子们要找工作的时候可以看看
图像细粒度分类是什么
不同于普通的分类任务,图像细粒度分类是指的对同一个大类别进行更加细致的分类,例如哈士奇与柯基。
RPN是怎么做的
有空补上
过拟合欠拟合是啥,怎么解决?
过拟合
过拟合是指训练误差和测试误差之间的差距太大。模型在训练集上表现很好,但在测试集上却表现很差,也就是泛化能力差。引起的原因有 ①训练数据集样本单一,样本不足 ②训练数据中噪声干扰过大 ③模型过于复杂。
防止过拟合的几种方法:
- 增加更多的训练集或者数据增强(根本上解决问题)
- 采用更简单点的模型(奥卡姆剃刀准则,简单的就是正确的)
- 正则化(L1,L2,Dropout)
- 可以减少不必要的特征或使用较少的特征组合
欠拟合
欠拟合是指模型不能在训练集上获得足够低的误差。换句换说,就是模型复杂度低,模型在训练集上就表现很差,没法学习到数据背后的规律。
欠拟合基本上都会发生在训练刚开始的时候,经过不断训练之后欠拟合应该不怎么考虑了。欠拟合可以通过使用非线性模型来改善,也就是使用一个更强的模型,并且可以增加训练特征
ResNet为啥能够解决梯度消失?怎么做的,能推导吗?
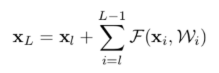
- 输入是x;
- F(x)相当于residual,它只是普通神经网络的正向传播;
- 输出是这两部分的加和H(x) = F(x)(就是residual) + x(就是shortcut,此代码shortcut部分做了一次卷积,也可以不做);
之所以可以避免梯度消失问题,是因为反向传播时,ε 代表的是 loss 方程,由链式求导法得:

可以看出,反向传播的梯度由2项组成的:
- 对x的直接映射,梯度为1;
- 通过多层普通神经网络映射结果为:
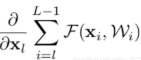 ;
;
即使新增的多层神经网络的梯度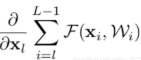 为0,那么输出结果也不会比传播前的x更差。同时也避免了梯度消失问题。
为0,那么输出结果也不会比传播前的x更差。同时也避免了梯度消失问题。
cxyzjd.com/article/qq_32172681/100177636
深度学习里面PCA的作用
PCA 用于降低维度,消除数据的冗余,减少一些不必要的特征。常用步骤如下(设有 m 条 n 维数据):
- 将原始数据按照列组成 m 行 n 列矩阵 X
- 将 X 的每一列(代表一个属性字段)进行零均值化(去中心化)减去这一列的均值得到特征中心化后的矩阵 $B = X_i - \mu_i$
- 求出协方差矩阵 $C = (X_i - \mu_i)*(X_i - \mu_i)^T$
-
求出矩阵 C 的特征值($det A-\lambda I =0$)和特征向量,按照特征值的大小将对应的特征向量从左往右排列,取前 k 个最大的特征值对应的特征向量组成矩阵 P - Y = PX 即为降维到 k 维后的数据,即从 n 维降到了 k 维,保留了原本的大部分信息
reference:
王兴政老师的PPT
https://blog.csdn.net/Virtual_Func/article/details/51273985
YOLOv3的框是怎么聚出来的?
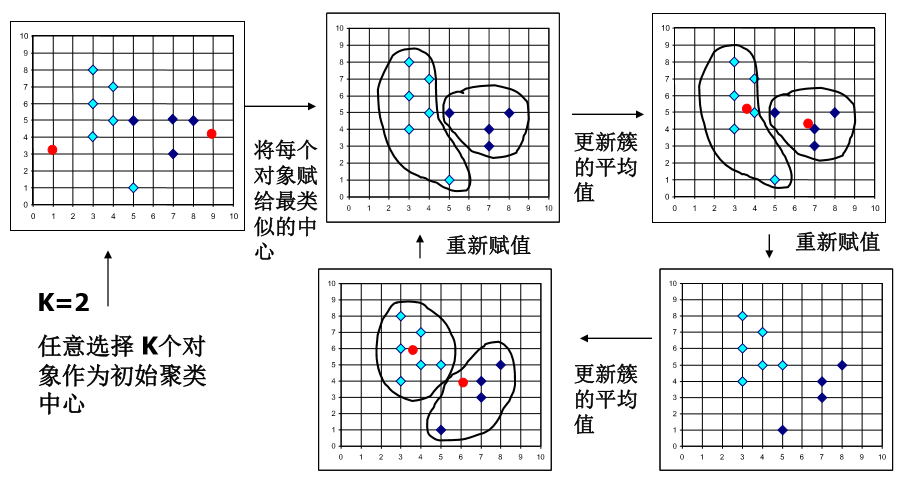
YOLOv3 的框是作者通过对自己的训练集的 bbox 聚类聚出来的,本质上就是一个 kmeans 算法,原理如下:
- 随机选取 k 个类别的中心点,代表各个聚类
- 计算所有样本到这几个中心点的距离,将每个样本归为距离最小的类别
- 更新每个类别的中心点(计算均值)
- 重新进行步骤 2 ,直到类的中心点不再改变
YOLOv3 的 kmeans 想法不能直接用 w 和 h 来作为聚类计算距离的标准,因为 bbox 有大有小,不应该让 bbox 的尺寸影响聚类结果,因此,YOLOv3 的聚类使用了 IOU 思想来作为距离的度量 \(d(bbox, centroid) = 1 - IOU(bbox, centroid)\) 也就是说 IOU 越大的话,表示 bbox 和 box_cluster 就越类似,于是将 bbox 划归为 box_cluster
在 AlexeyAB 大佬改进的 darknet 中实现了这个过程,具体就是加载所有训练集中的 bbox 的 w 和 h,随机选择 k 个作为 centroids,然后用所有样本去和这 k 个 centroids 做 IOU 得出距离,并将样本归为距离最小的 cluster,然后更新 centroids 重复上面的步骤,直到 centroids 不再更新
import numpy as np
def kmeans(boxes, k, dist=np.median):
"""
Calculates k-means clustering with the Intersection over Union (IoU) metric.
:param boxes: numpy array of shape (r, 2), where r is the number of rows
:param k: number of clusters
:param dist: distance function
:return: numpy array of shape (k, 2)
"""
rows = boxes.shape[0]
distances = np.empty((rows, k))
last_clusters = np.zeros((rows,))
np.random.seed()
# the Forgy method will fail if the whole array contains the same rows
# 随机 sample k 个 box 作为聚类中心
clusters = boxes[np.random.choice(rows, k, replace=False)]
while True:
for row in range(rows):
# 计算每一个 box 到聚类中心的距离(用 IOU 衡量距离)
distances[row] = 1 - iou(boxes[row], clusters)
# 选一个最近的聚类中心
nearest_clusters = np.argmin(distances, axis=1)
# 聚类中心不变的话就结束聚类
if (last_clusters == nearest_clusters).all():
break
for cluster in range(k):
# 根据聚类结果更新聚类中心
clusters[cluster] = np.median(boxes[nearest_clusters == cluster], axis=0)
last_clusters = nearest_clusters
return clusters
reference:
https://github.com/AlexeyAB/darknet/blob/master/scripts/gen_anchors.py
https://www.cnblogs.com/sdu20112013/p/10937717.html
YOLO和SSD的本质区别?
R-CNN系列和SSD本质有啥不一样吗?
SSD的致命缺点?如何改进
需要人工设置 prior box 的 min_size,max_size 和 aspect_ratio 值。网络中prior box的基础大小和形状不能直接通过学习获得,而是需要手工设置。而网络中每一层 feature 使用的 prior box 大小和形状恰好都不一样,导致调试过程非常依赖经验。 虽然采用了 pyramdial feature hierarchy 的思路,但是对小目标的 recall 依然一般,并没有达到碾压 Faster RCNN 的级别。作者认为,这是由于 SSD 使用 conv4_3 低级 feature 去检测小目标,而低级特征卷积层数少,存在特征提取不充分的问题。Kevin 补充:没错,SSD 的 anchor 设置导致 anchor 和小目标的 IoU 依然很小,大概只有 0.2 左右所以会漏掉很多小物体。 ———————————————— 版权声明:本文为CSDN博主「一个新新的小白」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/qq_31511955/article/details/80597211
SSD 的先验框和 Gt 框是怎么匹配的
在训练时 首先需要确定训练图片中的 ground truth 是由哪一个先验框来匹配,与之匹配的先验框所对应的边 界框将负责预测它。SSD 的先验框和 ground truth 匹配原则主要有 2 点。第一点是对于图片中的每个 ground truth,找到和它 IOU 最大的先验框,该先验框与其匹配,这样可以保证每个 ground truth 一 定与某个 prior 匹配。第二点是对于剩余的未匹配的先验框,若某个 ground truth 和它的 IOU 大于某 个阈值 (一般设为 0.5),那么这个先验框匹配这个 ground truth,剩下没有匹配上的先验框都是负样本(如果多个 ground truth 和某一个先验框的 IOU 均大于阈值,那么先验框只与 IOU 最大的那个进行匹配)。
怎么解决梯度消失和梯度弥散
YOLOv1到YOLOv3的发展历程以及解决的问题
FCOS 存在什么问题,如何解决
- 分配正负样本时,只要 anchor 在 gt_box 里面就算是正样本,这样会将很多背景区域也当成正样本,解决方式就是用 center_sampling,只在 gt_box 周围一个范围内的样本才是正样本。
- 原始论文中,为了解决网络在不同 FPN 层之间回归的距离差异太大,假设 FPN 某个 stride feature map 上某个点的回归预测值为 x,则对应的值为 $\exp^{S_i*x}$,使输出非负数,其中 $S_i$ 为当前尺度的一个可学习参数。这样做的话,用到指数函数,并且效果也不一定好,改进的点就是先将预测的距离通过一个 ReLU 使结果非负,然后在做标签的时候就将距离除以 stride,这样子的话每一层要回归的距离范围就差不多了,推理的时候只需要乘上 stride 就能还原真实 box 了。
- centerness 没什么作用,直接预测 IoU 代替。
- bbox loss weight 在原文中所有正样本的权重都是一样的,改进的话可以将该点的 centerness 值作为权重,越靠近中心点的 box 给越大的权重。
为什么分类要用交叉熵损失函数
说一下RCNN发展史
RCNN -> Fast RCNN -> Faster RCNN
#TODO
Faster RCNN
以经典的Faster R-CNN为例。整个网络可以分为两个阶段,training阶段和inference阶段
training 阶段,RPN 网络提出了 2000 左右的 proposals,这些 proposals 被送入到 Fast R-CNN 结构中,在 Fast R-CNN 结构中,首先计算每个 proposal 和 gt 之间的 iou,通过人为的设定一个 IoU 阈值(通常为 0.5),把这些 Proposals 分为正样本(前景)和负样本(背景),并对这些正负样本采样,使得他们之间的比例尽量满足(1:3,二者总数量通常为 128),之后这些 proposals(128 个)被送入到 Roi Pooling,最后进行类别分类和 box 回归。inference 阶段,RPN 网络提出了 300 左右的 proposals,这些 proposals 被送入到 Fast R-CNN 结构中,和 training 阶段不同的是,inference 阶段没有办法对这些 proposals 采样(inference 阶段肯定不知道 gt 的,也就没法计算 iou),所以他们直接进入 Roi Pooling,之后进行类别分类和 box 回归
NMS 的缺点以及改进工作
各种边缘检测算法的原理 (Sobel, Canny, Laplacian)
Sobel 算子
图像中的边缘部分的像素值变化剧烈,属于是高频的信息,提取边缘本质上就是对图像进行求导,OpenCV 中的 Sobel 算子就近似这个过程。因为噪声的区域的像素变化也很大,会对结果产生很大影响,所以我们首先要做的就是用高斯滤波将图像中的噪声过滤。然后对图像进行 x 和 y 方向上的求导(运用垂直和水平的奇数大小卷积模版对图像进行卷积)。得到图像在 x 和 y 方向上的梯度 Gx 和 Gy,然后得到总的梯度 $G = \sqrt{ G_{x}^{2} + G_{y}^{2} }$,有时为了节省开方带来的运算成本,我们直接把 Gx 和 Gy 相加得到梯度。(然后设定一个梯度阈值,大于这个阈值的被认为是边缘)。
Sobel 算子求的是一阶导数,后面有些边缘检测算子求的是二阶导数,并且 Sobel 在使用 3*3 卷积的时候效果没有 Scharr 滤波器更好,所以如果用 3*3 卷积核进行滤波的话尽量使用 Scharr 滤波器(卷积核的数值比 Sobel 更大)。
Laplacian 算子
laplacian 算子在 Sobel 的基础上进行改进,Sobel 那会儿已知图像的边缘部分是邻域梯度最大的部分,那么再对这个求一次导数呢,那么边缘部分的二阶导数就是 0 了。真不错,因此 laplacian 算子的原理就是对图像求二阶导数,不过预处理部分和 Sobel 差不多,也是要先转化成灰度图,再高斯滤波去除噪声,再进行求导操作。
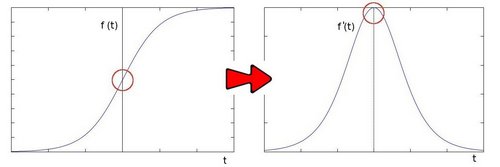
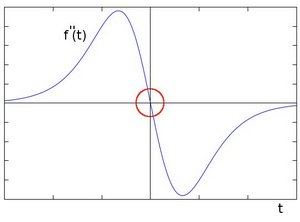
laplacian 算子运用的卷积核是如下数值的,因为还是求导数,所以内部调用的是 Sobel 函数。 \(\begin{bmatrix} 0 & +1 & 0 \\ 1 & -4 & 1 \\ 0 & +1 & 0 \end{bmatrix}\)
Canny 算子
Canny 算子是一种性能更好的算子,原理分为几步:
-
预处理(高斯去噪,灰度化)
-
对图像进行差分求导(Sobel)得到梯度方向和角度
-
进行极大值抑制去除真正的边缘周围的杂质得到比较好的边缘
-
这一步的目的是将模糊(blurred)的边界变得清晰(sharp)。通俗的讲,就是保留了每个像素点上梯度强度的极大值,而删掉其他的值。对于每个像素点,进行如下操作: a) 将其梯度方向近似为以下值中的一个(0,45,90,135,180,225,270,315)(即上下左右和 45 度方向)
b) 比较该像素点,和其梯度方向正负方向的像素点的梯度强度
c) 如果该像素点梯度强度最大则保留,否则抑制(删除,即置为 0)
-
-
双阈值筛选更精细的边缘

边缘 A 在 maxVal 之上,因此被认为是 “sure-edge”。尽管 C 边低于 maxVal 值,但它与 A 边相连,因此这条边也被认为是有效的我们得到了这条完整的曲线。但是 B 边,尽管它在 minVal以 上并且和 C 边在同一区域,但是它没有连接到任何 “sure-edge”,所以它被丢弃了。因此,为了得到正确的结果,我们必须相应地选择 minVal 和 maxVal,这是非常重要的。
关于相机标定以及姿态估计
相机内外参是什么意思
由于小孔成像原理,我们将现实生活中的一个点 P 投影到成像平面上 (中心为零点),成像点的坐标和 P 点真实坐标存在一个关系,和相机焦距有关,然后映射到成像平面还不够,我们还要将这个像给映射到像素坐标系 (u, v, 左上角为零点) 中,这个映射和像素坐标和 u 轴 v 轴的缩放系数以及原点平移的距离有关。将这些关系转化成矩阵可以得到下面的式子,
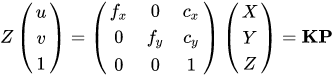
其中的 K 就是相机的内参,包含了焦距以及像素坐标系到相机坐标系 x 和 y 方向上的平移距离 (一般是分辨率的 1/2),这个用 MATLAB 对相机标定就可以获得,一般出厂之后就是固定的了,另外,相机标定除了内参矩阵以外还可以获得一个畸变矩阵,用来矫正相机的畸变。
外参指的是将一个点从世界坐标系 (三维)转变到相机坐标系 (二维) 所需要的旋转矩阵和平移矩阵,一般称为 R 和 t,有如下形式 \(\begin{align*} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix} &= \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*}\)
pnp 问题怎么解
https://docs.opencv.org/3.4/d5/d1f/calib3d_solvePnP.html
https://zhuanlan.zhihu.com/p/389653208
边框回归怎么做的,为什么需要 Encode
Most recently object detection programs have the concept of anchor boxes, also called prior boxes, which are pre-defined fix-sized bounding boxes on image input or feature map. The bounding box regressor, instead of predicting the bounding box location on the image, predicts the offset of the ground-truth/predicted bounding box to the anchor box. For example, if the anchor box representation is [0.2, 0.5, 0.1, 0.2], and the representation of the ground-truth box corresponding to the anchor box is [0.25, 0.55, 0.08, 0.25], the prediction target, which is the offset, should be [0.05, 0.05, -0.02, 0.05]. The object detection bounding box regressor is trying to learn how to predict this offset. If you have the prediction and the corresponding anchor box representation, you could easily calculate back to predicted bounding box representation. This step is also called decoding.
https://leimao.github.io/blog/Bounding-Box-Encoding-Decoding/
https://blog.csdn.net/zijin0802034/article/details/77685438
https://www.zhihu.com/question/370354869
有空写一下!!!!
gt 在做 loss 之前就已经和 Anchor 经过了 encode ,也就是从 Anchor 到 gt 所要经过的线性变换 (Gx, Gy, Gw, Gh),回归网络的输出就是这四个变换,也就是说网络在学习这种映射关系。所以网络的输出并不是真正的坐标,得到坐标只需要根据 encode 得到 decode 函数做一下解码就行了。
而且也不是所有的 Anchor 都参与了回归损失(拿 SSD 中的 8732 个 Anchor 和 smooth L1 来说),最终可以计算得到一个 pos_inx 代表正样本的索引,根据这个索引在 gt 和 Anchor 中找到对应的元素拿来做回归损失,因为负样本不用回归。
常见的Loss,回归的,分类的,Focal Loss
Sigmoid
\[\sigma=\frac{1}{1+e^-x}\]值域为(0,1)
Focal Loss
变形的交叉熵 \(CE = -\alpha(1-y_{pred})^\gamma log(y_{pred})\)
def FocalLoss(self, logit, target, gamma=2, alpha=0.5):
n, c, h, w = logit.size()
criterion = nn.CrossEntropyLoss(weight=self.weight, ignore_index=self.ignore_index,
size_average=self.size_average)
if self.cuda:
criterion = criterion.cuda()
logpt = -criterion(logit, target.long())
pt = torch.exp(logpt)
if alpha is not None:
logpt *= alpha
loss = -((1 - pt) ** gamma) * logpt
if self.batch_average:
loss /= n
return loss
reference: https://www.cnblogs.com/king-lps/p/9497836.html
FocalLoss 对样本不平衡的权重调节和减低损失值 - 知乎 (zhihu.com) 这个和 CE BCE 进行对比,比较清晰,但是这两个都是基于 softmax 的 FocalLoss,mmdet 中默认是基于 sigmoid 的 BCE loss 作为原型进行 FocalLoss 的。
softmax
常用于分类问题,在最后一层全连接之后用一个 softmax 将各神经元输出归一化到 0-1 之间,但总体相加的值还是等于 1
\[\sigma(Z)_j = \frac{e^{z_j}}{\sum^K_{k=1}e{z_k}}\]import numpy as np
z = np.array([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])
print(np.exp(z)/sum(np.exp(z)))
>>> [0.02364054 0.06426166 0.1746813 0.474833 0.02364054 0.06426166 0.1746813 ]
BCELoss
二分类常用的 loss,Binary CrossEntropyLoss,注意,在使用这个之前要使用 sigmoid 函数将预测值放到(0,1)之间
\[L = -\frac{1}{n}(ylog(y_{pred})+(1-y)log(1-y_{pred}))\]BCEWithLogitsLoss
这是集成了 sigmoid 和 BCELoss 的损失函数,一步到位
CrossEntropyLoss
\[CE = -\frac{1}{n}ylog(y_{pred})\]其中,$y_{pred}$ 又是网络输出通过一个 softmax 得到的值,也就是说函数会自动给他加一个 softmax 函数,所以最终公式就是
\[CE = -\frac{1}{n}ylog(\frac{e^{y_c}}{\sum_je^{y_j}})\]也就是 NLLLoss 和 LogSoftmax 两个函数的组合
>>> i = torch.randn(3,3)
>>> i
tensor([[-1.8954, -0.3460, -0.6694],
[ 0.5421, -1.1799, 0.8239],
[-0.0611, -0.8800, 0.8310]])
>>> label = torch.tensor([[0,0,1],[0,1,0],[0,0,1]])
>>> label
tensor([[0, 0, 1],
[0, 1, 0],
[0, 0, 1]])
>>> sm = nn.Softmax(dim=1)
>>> sm(i)
tensor([[0.1097, 0.5165, 0.3738],
[0.3993, 0.0714, 0.5293],
[0.2577, 0.1136, 0.6287]])
>>> torch.log(sm(i))
tensor([[-2.2101, -0.6607, -0.9840],
[-0.9180, -2.6400, -0.6362],
[-1.3561, -2.1751, -0.4640]])
>>> ll = nn.NLLLoss()
>>> target = torch.tensor([2,1,2])
>>> ll(torch.log(sm(i)), target)
tensor(1.3627)
>>> i
tensor([[-1.8954, -0.3460, -0.6694],
[ 0.5421, -1.1799, 0.8239],
[-0.0611, -0.8800, 0.8310]])
>>> los = nn.CrossEntropyLoss()
>>> los(i, target)
tensor(1.3627)
L1、L2范数是什么,区别呢?
范数是具有 “长度” 概念的函数。在向量空间内,为所有的向量的赋予非零的增长度或者大小。不同的范数,所求的向量的长度或者大小是不同的。举个例子,2 维空间中,向量 (3,4) 的长度是 5,那么 5 就是这个向量的一个范数的值,更确切的说,是欧式范数或者L2范数的值。
更一般的情况下,对于一个 p- 范数,如果 $x = [x_1, x_2, x_3, …, x_n]^T$, 那么向量 x 的 p- 范数就是 $$ \begin{equation}
| x | _p = ( | x_1 | ^p+ | x_2 | ^p+…+ | x_n | ^p)^{1/p} |
\end{equation} \(那么 L1 范数就是 p 为 1 的时候,也就是向量内所有元素的绝对值之和:\) \begin{equation}
| x | _p = ( | x_1 | + | x_2 | +…+ | x_n | ) |
\end{equation} \(L2 范数就是向量内所有元素的平方相加然后再开方:\) \begin{equation}
| x | _p = ( | x_1 | ^2+ | x_2 | ^2+…+ | x_n | ^2)^{1/2} |
\end{equation} $$ 特别的,L0 范数是指向量中非零元素的个数!
在深度学习中,常常会在最后的 loss 函数中加一个正则项,将模型的权重 W 作为参数传入范数中,为的就是防止模型参数过大,这样可以防止过拟合发生。
reference:
https://zhuanlan.zhihu.com/p/28023308
https://www.cnblogs.com/LXP-Never/p/10918704.html(解释得挺好的,借鉴了下面这篇文章)
http://www.chioka.in/differences-between-l1-and-l2-as-loss-function-and-regularization/#
https://wangjie-users.github.io/2018/11/28/%E6%B7%B1%E5%85%A5%E7%90%86%E8%A7%A3L1%E3%80%81L2%E8%8C%83%E6%95%B0/
pooling layer怎么反向传播
池化层没有可以训练的参数,因此在卷积神经网络的训练中,池化层只需要将误差传递到上一层,并不需要做梯度的计算。要追求一个原则,那就是梯度之和不变。
- average pooling
直接将梯度平均分到对应的多个像素中,可以保证梯度之和是不变的
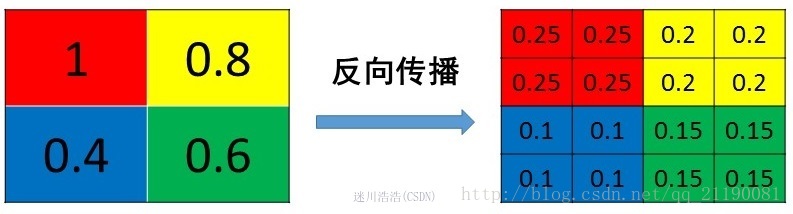
- max pooling
max pooling要记录下最大值像素的index,然后在反向传播时将梯度传递给值最大的一个像素,其他像素不接受梯度,也就是为0
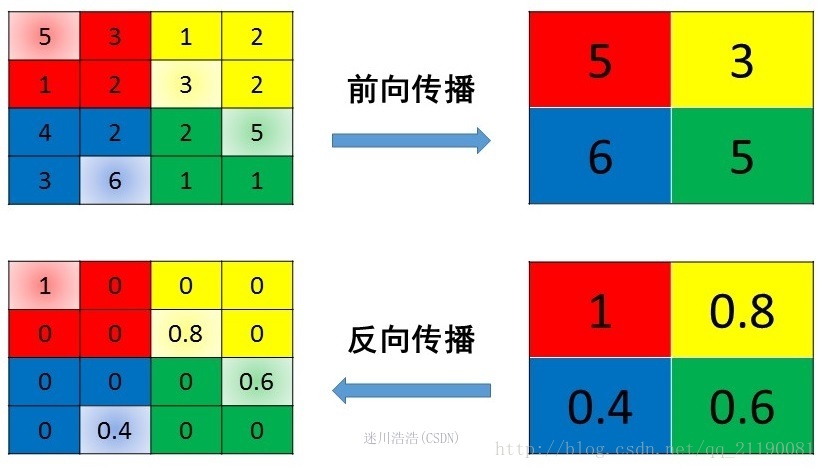
reference: https://blog.csdn.net/qq_21190081/article/details/72871704
MobileNet在特征提取上有什么不同
MobileNet 用的是深度可分离卷积(Depthwise separable convolution),将传统的卷积分成了 Depthwise convolution 和 Pointwise convolution,也就是先对每个通道进行单独的卷积,不把这些特征组合在一起,然后用 Pointwise convolution 也就是一个 1* 1 卷积核将通道特征组合在一起,这样可以大大减少模型的参数量以及运算量,适合运用于嵌入式设备等对延时和性能要求较高的场景中。
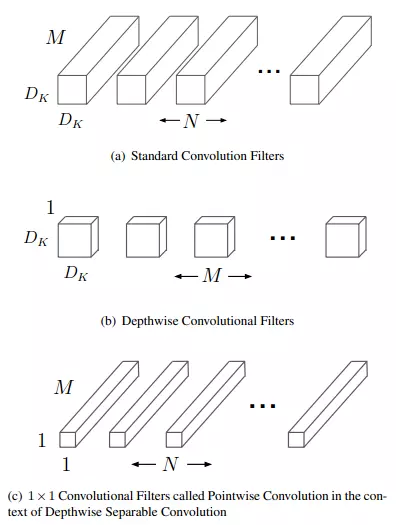
图 (a) 代表标准卷积。假设输入特征图尺寸为 ,卷积核尺寸为
,输出特征图尺寸为
,标准卷积层的参数量为:
。
图 (b) 代表深度卷积,图 (c) 代表逐点卷积,两者合起来就是深度可分离卷积。深度卷积负责滤波,尺寸为 (DK,DK,1),共M个,作用在输入的每个通道上;逐点卷积负责转换通道,尺寸为 (1,1,M),共 N 个,作用在深度卷积的输出特征映射上。
深度卷积参数量为 ,逐点卷积参数量为
。用了深度可分离卷积所需要的参数量和普通卷积的参数量如下,在 MobileNet 中,卷积核的尺寸 $D_K$ 为 3 * 3,因此这样的参数量相当于减少了 9 倍
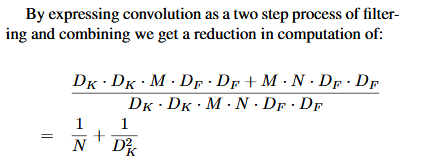
Depthwise convolution 的实现是通过 nn.Conv2d 中的 groups 参数,这个数字要能被 in_channels 和 out_channels 整除,一般来说,Depthwise convolution 中的第一个 Group convolution 的输入输出通道都是一样的,pointwise convolution 才是起到改变维度的作用。下面例子中通过通道可分离卷积保存的模型比标准卷积更小 (47KB VS 362KB)
import torch.nn as nn
class Normal(nn.Module):
def __init__(self, i, o, k):
super(Normal, self).__init__()
self.conv = nn.Conv2d(i, o, k, padding=k // 2)
def forward(self, x):
x = self.conv(x)
return x
class DepwiseSeparable(nn.Module):
def __init__(self, i, o, k):
super(DepwiseSeparable, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(i, i, k, groups=i, padding=k // 2),
nn.Conv2d(i, o, 1)
)
def forward(self, x):
x = self.conv(x)
return x
normal = Normal(100, 100, 3)
dep = DepwiseSeparable(100, 100, 3)
torch.save(normal, 'normal.pth')
torch.save(dep, 'dep.pth')
我们可以通过另外一个实验说明深度可分离卷积的优越性
conv = nn.Conv2d(in_channels=6, out_channels=6, kernel_size=1, groups=1)
conv.weight.data.size()
-> torch.Size([6, 6, 1, 1])
conv = nn.Conv2d(in_channels=6, out_channels=3, kernel_size=1, groups=1)
conv.weight.data.size()
-> torch.Size([3, 6, 1, 1])
说明 conv.weights.data.size() 的内容为 (out_channels, in_channels, kernel_size, kernel_size),我们设置不同的 groups 看看结果
conv = nn.Conv2d(in_channels=6, out_channels=6, kernel_size=1, groups=2)
conv.weight.data.size()
-> torch.Size([6, 3, 1, 1])
conv = nn.Conv2d(in_channels=6, out_channels=6, kernel_size=1, groups=3)
conv.weight.data.size()
-> torch.Size([6, 2, 1, 1])
conv = nn.Conv2d(in_channels=6, out_channels=6, kernel_size=1, groups=6)
conv.weight.data.size()
-> torch.Size([6, 1, 1, 1])
所以当 group=1 时,该卷积层需要 6*6*1*1=36 个参数,即需要 6 个 6*1*1 的卷积核。计算时就是 6*H_in*W_in 的输入整个乘以一个 6*1*1 的卷积核,得到输出的一个 channel 的值,即 1*H_out*W_out。这样经过 6 次与 6 个卷积核计算就能够得到 6*H_out*W_out 的结果了。
如果将 group=3 时,卷积核大小为 torch.Size([6, 2, 1, 1]),即 6 个 2*1*1 的卷积核,只需要 6*2*1*1=12 个参数。那么每组计算就只被 in_channels/groups=2 个 channels 的卷积核计算,其实就相当于是将 6*H_in*W_in 大小的输入按 channels 分成 3 分,每份大小为 2*H_in*W_in,6 个卷积核也会对应分成 3 份,即 2*1*1,每份输入对应每份卷积核。所以将每份输入 2*H_in*W_in 看成一个输入,应用 2 个 2*1*1 的卷积核,就能够得到 2*H_out*W_out。一份得到一个 2*H_out*W_out 的输出,那么 3 份就能够得到 3 个 2*H_out*W_out 的输出,在 channels 维 concat 起来得到最后的 6*H_out*W_out 输出。
为什么用smooth L1 loss,和L1 loss、L2 loss有啥区别?
先看 L1 loss 的公式为 $|y_{pred} - y|$,L2 loss 的公式为$|y_{pred} - y|^2$ ,smooth L1 loss 的公式是 $SmoothL1(x)=
\begin{cases}
0.5x^2& \text{|x| < 1}
|x| - 0.5 & \text{|x| > 1}
\end{cases}$,根据 fast rcnn 的说法,”…… L1 loss that is less sensitive to outliers than the L2 loss used in R-CNN and SPPnet.” 也就是 smooth L1 loss 让 loss 对于离群点更加鲁棒,即:相比于 L2 损失函数,其对离群点、异常值(outlier)不敏感,梯度变化相对更小,训练时不容易跑飞。但是我的理解是 SmoothL1 loss 能够让训练时对和 gt 比较相近的结果的惩罚更小,使得 loss 收敛得更加稳定,对更远的结果惩罚更大,有点困难样本挖掘的意思。
关于数据集的一些碎碎的知识点
COCO
coco2017 有 118287 张训练集,5000 张验证集,40670 张测试集
Pascal VOC
VOC 语义分割时,之前一直不知道 gt 和 output 是怎么做 loss 的,记录一下。一共有 20 个类,gt_mask 是一张 8 位的 png 彩图,虽然是 8 位,但是他其实有 RGB 值,用 ps 打开的话可以直接看到各个像素的 RGB 值,这时你会怀疑这是个三通道的彩图,其实不是,用 PIL 打开 mask 的时候,打印 shape 会发现他就是单通道的图,将其像素值打印出来又会发现,大多数都是 0,而且基本不会超过 20,但是有些会到 255,这是因为,看下图好了,白色的区域是不计算 loss 的,在损失函数里面表现为 ignore_index=255,然后黑色部分像素为 0,代表背景,所以网络最后的输出其实有 21 个通道。其余对应的颜色的像素值就代表的这个类别的 label,之前我还一直在想他到底是怎么将颜色值转化成 label 的,原来 PIL 读进来就直接是 label 了,我裂开
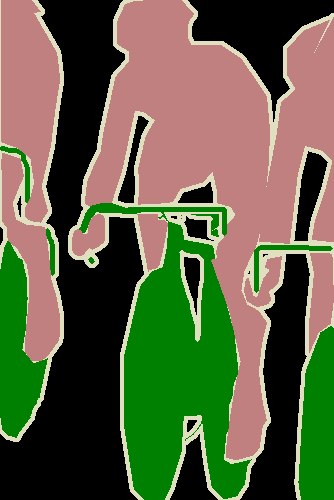
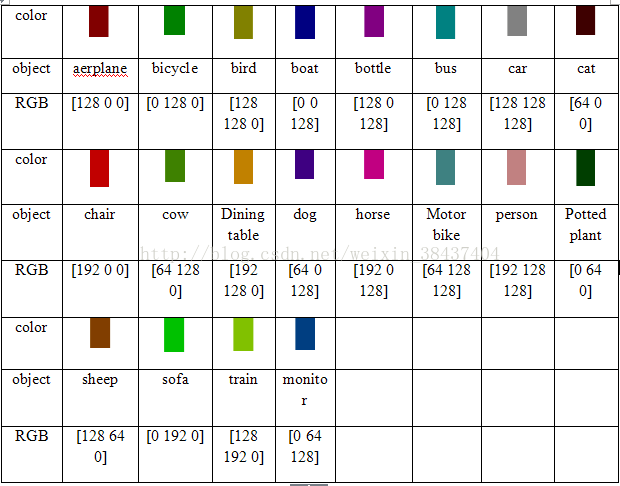
reference: https://blog.csdn.net/weixin_38437404/article/details/78788250
目标检测中有些代码在训练时会将模型的 BN 层给冻结,这是为什么?
目标检测中一般会用到在 ImageNet 上预训练好的分类器权重,别人的 batch_size 很大,所以对 BN 层应该训练出了一个比较不错的参数(γ 和 β),而目标检测的 batch_size 可能没有那么大,可能 minibatch 不足以反映出样本整体的分布,训练出来的参数不一定有别人好,所以冻结住 BN 说不定会使模型表现更好
def freeze_bn(self):
'''Freeze BatchNorm layers.'''
for layer in self.modules():
if isinstance(layer, nn.BatchNorm2d):
layer.eval()
It’s a common practice to freeze BN while training object detection models. This is done because you usually start from some Imagenet pre-trained weights which were trained with large BS (like 256 or larger) while in object detection BS is much smaller. You don’t want to ruin good pretrained statistics so freezing BN is a good idea
https://github.com/yhenon/pytorch-retinanet/issues/151
各种卷积
分组卷积
分组卷积最早在 AlexNet 中出现,当时作者在训练模型时为了减少显存占用而将 feature map 分组然后给多个 GPU 进行处理,最后把多个输出进行融合。具体计算过程是,分组卷积首先将输入 feature map 分成 g 个组,每个组的大小为 (1, iC/g, iH, iW),对应每组中一个卷积核的大小是 (1,iC/g,k,k),每组有 oC/g 个卷积核,所以每组输出 feature map 的尺寸为 (1,oC/g,oH,oW),最终 g 组输出拼接得到一个 (1,oC,oH,oW) 的大 feature map,总的计算量为 iC/g×k×k×oC×oH×oW,是标准卷积的 1/g,参数量也是标准卷积的 1/g。
但由于 feature map 组与组之间相互独立,存在信息的阻隔,所以 ShuffleNet 提出对输出的 feature map 做一次 channel shuffle 的操作,即通道混洗,打乱原先的顺序,使得各个组之间的信息能够交互起来
空洞卷积
空洞卷积是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。通过间隔取值扩大感受野,让原本 3x3 的卷积核,在相同参数量和计算量下拥有更大的感受野。这里面有个扩张率 (dilation rate) 的系数,这个系数定义了这个间隔的大小,标准卷积相当于 dilation rate 为 1 的空洞卷积,下图展示的是 dilation rate 为 2 的空洞卷积计算过程,可以看出3×3的卷积核可以感知标准的 5×5 卷积核的范围,还有一种理解思路就是先对 3×3 的卷积核间隔补 0,使它变成 5×5 的卷积,然后再执行标准卷积的操作。

reference: https://mp.weixin.qq.com/s/LO1W2saWslf6Ybw_MZAuQQ
转置卷积
转置卷积又称反卷积 (Deconvolution),它和空洞卷积的思路正好相反,是为上采样而生,也应用于语义分割当中,而且他的计算也和空洞卷积正好相反,先对输入的 feature map 间隔补 0,卷积核不变,然后使用标准的卷积进行计算,得到更大尺寸的 feature map。
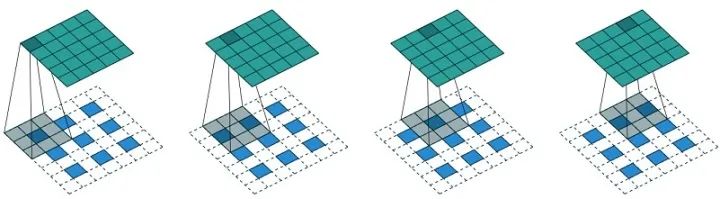
可变形卷积
以上的卷积计算都是固定的,每次输入不同的图像数据,卷积计算的位置都是完全固定不变,即使是空洞卷积/转置卷积,0 填充的位置也都是事先确定的。而可变形卷积是指卷积核上对每一个元素额外增加了一个 h 和 w 方向上偏移的参数,然后根据这个偏移在 feature map 上动态取点来进行卷积计算,这样卷积核就能在训练过程中扩展到很大的范围。而显而易见的是可变形卷积虽然比其他卷积方式更加灵活,可以根据每张输入图片感知不同位置的信息,类似于注意力,从而达到更好的效果,但是它比可变形卷积在增加了很多计算量和实现难度,目前感觉只在 GPU 上优化的很好,在其他平台上还没有见到部署。
loss 出现 NaN 怎么解决
NaN 可以看成是无穷大或者无穷小,经常是由于在网络计算 loss 的时候除以 0 或者 log(0) 导致的,如果是这种原因的话就得检查代码是否正确,一般在 loss 除以正样本的时候会加个 eps=0.0001 来防止出现 NaN,但如果代码没有问题的话可能就是梯度爆炸了,变得很大,这时候要么就做个梯度裁剪(梯度大于某个值就不要了),或者降低学习率让网络每一步更新的梯度不要太夸张
matting 跟 segmentation 有什么区别
segmentation 就是对图片中的每一个像素进行分类,判断其所属概率最大的类别。抠图比分割更加严格, 在抠图中有一个公式 I = αF + (1-α)B。我们需要是把 α(不透明度)、F(前景色)和B(背景色)三个变量给解出来。和其它图片进行融合的时候,就会用到 α(不透明度),它可以使得融合效果特别自然,就像 PS 的羽化边缘。
feature map 上的像素怎么映射到原图的
根据感受野,例如通过一层层卷积最终被 stride 16 的 feature map,该层的感受野是 31,因此映射回原图的话相当于一个像素点对应原图的 31x31 的区域,能够看到更广的区域,并不是单纯的对应 16x16 的区域。
↓↓↓↓↓以下为收集到的面试题↓↓↓↓↓
mAP 计算公式
mmdetection 中,将结果送去计算 mAP 之前,先调用了 bbox_head 的 get_bbox,这个函数默认用了 test_cfg 中的 nms_cfg,也就是会先将得到的 bbox 进行一个类间的 nms 筛除掉一些重复的框再送入 evaluator
通用流程为以下:
- 送去计算 mAP 之前先经过 nms 将 box 给筛一遍(optional)
- 再将整个数据集的 box 按照 confidence 从高到低进行排序
- 对每个类别计算 AP:
- 取预测为该类别的 box,记录下每一个 box 对应的 image id,confidence,与 image id 那张图中的所有gt_box 求得的 max_iou,以及与之匹配的 gt_box 的 index,然后判定这个 box 是 FP 还是 TP
- 如果 max_iou 大于 IOU 阈值,则 box 是 TP,反之为 FP,但是如果与这个 box 计算所得的 IOU 最大的 gt_box 已经跟其他 box 计算过了的话,那么这个 box 是 FP,因为一个 gt_box 只能匹配一个 box
- 累加之前计算出的 FP、TP 和当前的 FP、TP,可以得到每一次迭代的 precision 和 recall
- P = TP / (TP + FP) 分母代表所有 predictions,R = TP / (TP + FN) 分母代表所有 gt_boxes
- 以 P 为纵轴,R 为横轴,根据 P R 点画图,将图像插值为一个个长方形柱,计算面积。(COCO 的做法是取 101 个点进行 AP 的计算)
- 平均一下所有类别的 AP,得到该 IOU 阈值下的 AP
- 更换 IOU 阈值,得到不同阈值下的 AP,对这些 AP 进行平均得到 mAP
SENet 实现细节
SoftNMS 的优缺点
原理:
NMS 直接将和得分最大的 box 的 IOU 大于某个阈值的 box 的得分置零,很粗暴,Soft NMS 就是用稍低一点的分数来代替原有的分数,而不是直接置零
优点:
仅需要对传统的 NMS 算法进行简单的改动且不增额外的参数
Soft-NMS 具有与传统NMS 相同的算法复杂度,使用高效
Soft-NMS 不需要额外的训练,并易于实现,它可以轻松的被集成到任何物体检测流程中
缺点:
还是得人工设置置信度的阈值筛选最后保留的框(一般是 0.0001)
对二阶段友好,对很多一阶段的算法没什么用
ROI Pooling 的计算过程
ResNet 和 ResNext 的区别
anchor_box 如何恢复到原始的大小
Corner Pooling 的作用
通过显式地将物体地特征集中到两个角点,给网络添加了一些先验信息,让网络更快收敛。通过 Corner Pooling,直接使网络增加了两个百分点的性能。(Corner Pooling 的思想真的不错,让网络提前知道自己应该学什么,而不是通过 GT 硬学,相当于课前预习了一下!)
##模型压缩的主要方法有哪些
- 从模型结构上来说分为:模型剪枝,模型蒸馏,NAS 自动学习模型结构等.
- 模型参数量化上包括数值精度量化到 FP16 等.
IOU-aware 的思想是什么
IOU-aware 的思想就是在一阶段检测器进行检测时,头部的回归分支和分类分支经常是单独计算的,两者并没有什么关联性,也就是说当一个 anchor 的置信度很高时,网络并不知道他回归的好不好,也就是不知道这个框的质量。因此,就如果我们能将置信度和框的质量相联系起来的话就可以得到更好的结果。这就是 IOU-aware 的由来,具体思想就是在回归分支上再加一个 IOU 分之来预测当前 prediction 和 gt 的 IOU (需要经过一个 sigmoid 归一化到 0-1),IOU 分支的标签就是当前位置 anchor 和相对应的 gt 的 IOU,作者在论文中使用的是 BCE loss。mmdet 中的实现如下:
pred_box = delta2bbox(level_anchor, bbox_pred, self.target_means, self.target_stds)
# the negatives will stores the anchors information(x, y, w, h)
target_box = delta2bbox(level_anchor, bbox_targets, self.target_means, self.target_stds)
iou = bbox_overlaps(target_box, pred_box, is_aligned=True) # (batch*width_i*height_i*A)
iou_pred = iou_pred.permute(0, 2, 3, 1).reshape(-1) # (batch*width_i*height_i*A)
loss_iou = weight_iou*weighted_iou_regression_loss(iou_pred, iou, bbox_weight, avg_factor=num_total_samples)

各种算法对正负样本的定义是怎样的
TODO,加上 PAA,autoassign,以及最新的一些 cost function 的算法
(1) faster rcnn和retinanet系列采用通用的iou阈值来区分正负样本,不够鲁棒
(2) dynamic rcnn通过在训练中自适应的提高iou阈值来动态改变正负样本定义,算是一个不错的改进
(3) fcos采用的是回归范围限制和中心扩展系数超参来区分正负样本,超参难以设置
(4) atss提出了基于每层候选anchor,然后计算均值和方差来自适应的计算正负样本,虽然超参就一个但是其实有先验即物体越靠近中心越有可能是正样本,没有做到基于预测值进行自适应功能
(5) yolov3和v4系列采用了iou和网格约束先验来区分正负样本,而v5创新性的采用了宽高比例和邻近网格约束进行区分
2022.3.10 更新面经题目
| https://leetcode-cn.com/circle/discuss/QmTRU4/ |
BatchNorm 在 train 和 test 的时候有什么不同
高频滤波,低频滤波是什么
TODO
图像滤波是一种非常重要的图像处理技术,现在大火的卷积神经网络其实也是滤波的一种,都是用卷积核去提取图像的特征模式。不过,传统的滤波,使用的卷积核是固定的参数,是由经验丰富的人去手动设计的,也称为手工特征。而卷积神经网络的卷积核参数是未知的,是根据不同的任务由数据驱动去学习得到的参数,更能适应于不同的任务。
口述反向传播过程
信号前向传播,误差反向传播。前项过程中通过与正确的标签计算损失,反向传递损失,更新参数,优化至最后的参数。
神经网络的损失函数为什么是非凸的
空洞卷积为啥会有用,和大 kernel 的卷积有什么不同?
特征图相同情况下,空洞卷积可以得到更大的感受野,从而获得更加密集的数据。更大的感受野可以提高在目标检测和语义分割的任务中的大物体识别分割的的效果。当网络层需要更大的感受野,但是由于计算资源有限无法提高卷积核数量或大小时,可以考虑使用空洞卷积。
空洞卷积存在的问题?
当多次叠加扩张率为 3*3 的 kernel 时,会产生网格效应,也就是说并不是所有的 pixel 都拿来计算了,这样的方式会损失信息的连续性,对于像素级的任务来说是致命的。可以通过修改扩张率来缓解这种现象(如 [1,2,5,1,2,5])。
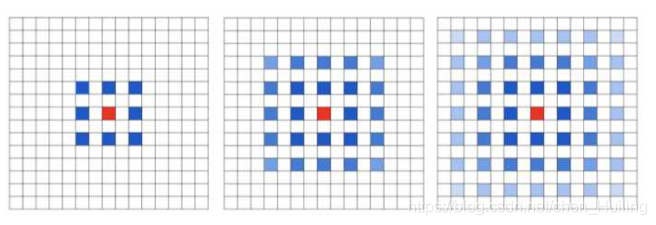
https://blog.csdn.net/chen_Huiling/article/details/112632740
torch.jit.trace 和 torch.jit.script 的区别
这是将 PyTorch 模型转化成 TorchScript 格式的两种方法,有些差别
- trace 只记录走过的 tensor 和对 tensor 的操作,不会记录任何控制流信息,如 if 条件句和循环。因为没有记录控制流的另外的路,也没办法对其进行优化。好处是 trace 深度嵌入 python 语言,复用了所有 python 的语法,在计算流中记录数据流。
- script 会去理解所有的 code,真正像一个编译器一样去进行 lexer、parser、Semantic analusis 的分析「也就是词法分析语法分析句法分析,形成 AST 树,最后再将 AST 树线性化」。script 相当于一个嵌入在 Python/Pytorch 的 DSL,其语法只是 pytorch 语法的子集,这意味着存在一些 op 和语法 script 不支持,这样在编译的时候就会遇到问题。此外,script 的编译优化方式更像是 CPU 上的传统编译优化,重点对于图进行硬件无关优化,并对 if、loop 这样的 statement 进行优化。
解决方法是将这两种方式混合使用,最终转的时候用 script,但是中间可以对一些东西加上 trace 的装饰器。
https://zhuanlan.zhihu.com/p/410507557
Conv BN ReLU 怎样融合
这里假定是网络的某一激活层特征,我们要对其进行归一化。若模型训练batch中共有
个样例,其特征分别是
,我们采用下列公式进行归一化:
这里和
为这个batch上计算得到的均值和方差(在B,H,W维度上计算,每个channel单独计算),而
防止除零所设置的一个极小值,
是放缩系数,而
是平移系数。在训练过程中,
and
在当前batch上计算:
而参数和
是和其它模型参数一起通过梯度下降方法训练得到。在测试阶段,我们不太会对一个batch图像进行预测,一般是对单张图像测试。因此,通过前面公式计算
and
就不可能。BN的解决方案是采用训练过程中指数移动平均值
和
。
目前,BN层大部分用于CNN网络中,此时上面的4个参数就是针对特征图各个通道的参数,这里我们记,
,
以及
为第
个通道的参数。
融合方案
首先我们将测试阶段的 BN 层(一般称为 frozen BN)等效替换为一个 1x1 卷积层:
对于一个形状为 的特征图
,归一化后的结果
,可以如下计算:
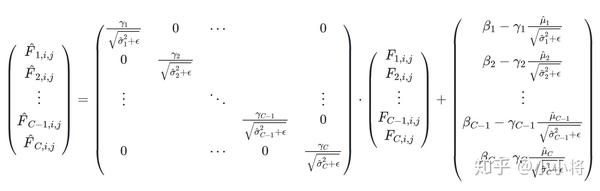
这里的 是特征图的各个空间位置,我们可以看到上述计算就是
形式,其可以看成是
卷积(只不过每一个通道都只有一个地方是有值的),这里 W 的行向量就是每个对应输出通道的卷积核(
)。由于 BN 层常常在 Conv 层之后,我们可以进行两个操作的合并。
然后我们将 BN 层和 Conv 层融合: 这里我们记:
和
为BN的参数,
和
是BN前面Conv层的参数,
为Conv层的输入,
为输入层的channel数,
是Conv层的卷积核大小
我们将的每个卷积
部分reshape为一个维度为
的向量
,因此Conv层加BN层的操作为:
显然,我们可以将Conv层和BN层合并成一个新的卷积层,其参数为:
- filter weights:
- bias:
最后我们在PyTorch中实现这个融合操作:(计算权重的时候用 troch.mm 矩阵相乘)
def fuse(conv, bn):
fused = torch.nn.Conv2d(
conv.in_channels,
conv.out_channels,
kernel_size=conv.kernel_size,
stride=conv.stride,
padding=conv.padding,
bias=True
)
# setting weights
w_conv = conv.weight.clone().view(conv.out_channels, -1)
w_bn = torch.diag(bn.weight.div(torch.sqrt(bn.eps+bn.running_var)))
fused.weight.copy_( torch.mm(w_bn, w_conv).view(fused.weight.size()) )
# setting bias
if conv.bias is not None:
b_conv = conv.bias
else:
b_conv = torch.zeros( conv.weight.size(0) )
b_conv = torch.mm(w_bn, b_conv.view(-1, 1)).view(-1)
b_bn = bn.bias - bn.weight.mul(bn.running_mean).div(
torch.sqrt(bn.running_var + bn.eps)
)
fused.bias.copy_( b_conv + b_bn )
return fused
https://zhuanlan.zhihu.com/p/110552861
TensorRT 加速的原理是什么
移动端模型压缩部署有哪些方法
- 剪枝蒸馏
- 使用 trt、ncnn 等框架
- 量化(FP16,INT8)
https://github.com/scutan90/DeepLearning-500-questions/blob/master/ch17%E6%A8%A1%E5%9E%8B%E5%8E%8B%E7%BC%A9%E3%80%81%E5%8A%A0%E9%80%9F%E5%8F%8A%E7%A7%BB%E5%8A%A8%E7%AB%AF%E9%83%A8%E7%BD%B2/%E7%AC%AC%E5%8D%81%E4%B8%83%E7%AB%A0%E6%A8%A1%E5%9E%8B%E5%8E%8B%E7%BC%A9%E3%80%81%E5%8A%A0%E9%80%9F%E5%8F%8A%E7%A7%BB%E5%8A%A8%E7%AB%AF%E9%83%A8%E7%BD%B2.md
归一化和标准化什么区别
当原始数据不同维度特征的尺度(量纲)不一致时,需要标准化步骤对数据进行标准化或归一化处理。
归一化 就是将训练集中某一列数值特征(假设是第 i 列)的值缩放到 0 和 1 之间。方法如下所示:
|  |
标准化 就是将训练集中某一列数值特征(假设是第i列)的值缩放成均值为 0,方差为 1 的状态(不一定是正态分布,取决于特征原来的分布)。如下所示:
|  |
python 中 array 和 list 的区别
list 可以存放不同类型的数据,array 只能存放相同类型的数据
数据不均衡问题怎么解决
mobilenet V1 V2 的优缺点
10000 类的分类问题应该怎么做
用树形图来分类,参考 YOLO-9000
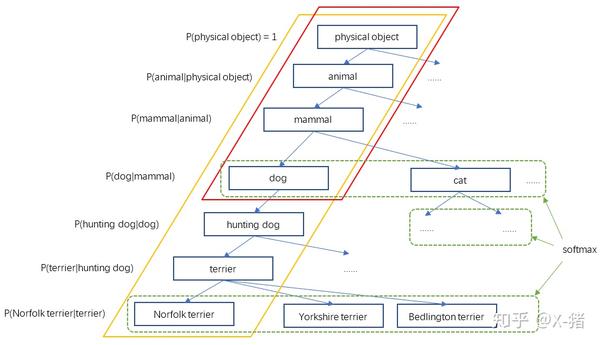
整个WordTree中的对象之间不是互斥的关系,但对于单个节点,属于它的所有子节点之间是互斥关系。比如terrier节点之下的Norfolk terrier、Yorkshire terrier、Bedlington terrier等,各品种的terrier之间是互斥的,所以计算上可以进行softmax操作。上面图10只画出了3个softmax作为示意,实际中每个节点下的所有子节点都会进行softmax。
BN 为什么要重构
为了恢复出原始的某一层所学到的特征。因此我们引入了这个可学习重构参数 γ、β,让我们的网络可以学习恢复出原始网络所要学习的特征分布。
数据并行和模型并行有什么区别
数据并行:
每一个节点(或者叫进程)都有一份模型,然后各个节点取不同的数据,通常是一个 batch_size,然后各自完成前向和后向的计算得到梯度,这些进行训练的进程我们成为 worker,除了 worker,还有参数服务器,简称 ps server,这些 worker会把各自计算得到的梯度送到 ps server,然后由 ps server 来进行 update 操作,然后把 update 后的模型再传回各个节点。因为在这种并行模式中,被划分的是数据,所以这种并行方式叫数据并行。
模型并行:
深度学习的计算其实主要是矩阵运算,用 GPU 卡计算的话就是放在显存里,可是有的时候矩阵会非常大,比如在 CNN 中如果 num_classes 达到千万级别,那一个 FC 层用到的矩阵就可能会大到显存塞不下。这个时候就不得不把这样的超大矩阵给拆了分别放到不同的卡上去做计算,从网络的角度来说就是把网络结构拆了,其实从计算的过程来说就是把矩阵做了分块处理。
有的时候呢数据并行和模型并行会被同时用上。比如深度的卷积神经网络中卷积层计算量大,但所需参数系数 W 少,而 FC 层计算量小,所需参数系数 W 多。因此对于卷积层适合使用数据并行,对于全连接层适合使用模型并行。
Reference: https://www.zhihu.com/question/53851014
🌟手撸深度学习算子 / 传统图像处理
sobel 算子 (jeffin)
# 手动卷积 (Sobel算子)
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread(r"C:\Users\Jeffin_\Desktop\pic.jpg", 0)
img = cv2.resize(img, (256,256), cv2.INTER_LINEAR)
cv2.imshow('test', img)
def sobel_x(img):
h, w = img.shape
Newimg_X = np.zeros_like(img)
sobel_X = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
for j in range(w-2):
for i in range(h-2):
Newimg_X[i+1, j+1] = abs(np.sum(img[i:i+3, j:j+3] * sobel_X))
return np.uint8(Newimg_X)
def sobel_y(img):
h, w = img.shape
Newimg_Y = np.zeros_like(img)
sobel_Y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
for j in range(w-2):
for i in range(h-2):
Newimg_Y[i+1, j+1] = abs(np.sum(img[i:i+3, j:j+3] * sobel_Y))
return np.uint8(Newimg_Y)
直方图均衡化
img = cv2.imread('imgs/wild.jpeg', 0) # 1. 读取灰度图
prob = np.array([np.sum(img == i) for i in range(256)])
r, c = img.shape
# 2. 得到每一个像素出现的概率
prob = prob / (r * c)
plot(prob, "原图直方图")
# 3. 直方图均衡化
prob = np.cumsum(prob) # 3.1 累计概率
img_map = [int(i * prob[i]) for i in range(256)] # 3.2 像素值映射(要记住!)
# 3.3 像素值替换
for ri in range(r):
for ci in range(c):
img[ri, ci] = img_map[img[ri, ci]]
prob = np.array([np.sum(img == i) for i in range(256)])
r, c = img.shape
prob = prob / (r * c)
plot(prob, "直方图均衡化结果")
plt.figure()
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.show()
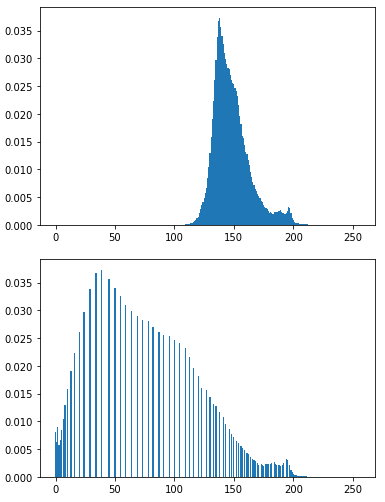
公式推导:https://zhuanlan.zhihu.com/p/44918476
求 Tensor 每个像素与其他像素之间的自相似度
# 计算 2D 或者 4D tensor 相似度
import torch
def sim(query, key, eps = 1e-8):
input_dim = query.dim()
assert query.dim() == key.dim()
if (input_dim == 4):
B, C, H, W = query.shape
query = query.reshape(B, C, -1) # B,C, H*W
# 用 permute 会出错,因为只是转置一部分
query = F.normalize(query, p=2, dim=1, eps=eps).transpose(1,2) # B, H*W, C
key = key.reshape(B, C, -1) # B, C, H*W
key = F.normalize(key, p=2, dim=1, eps=eps)
similarity = torch.matmul(query, key) # B, H*W, H*W
assert similarity.max() < 1.001 and similarity.min() > -1.001, 'cosine similarity ranges [-1, 1]'
return similarity
elif input_dim == 2:
B, C = query.shape
# 用 permute 会出错,因为只是转置一部分
query = F.normalize(query, p=2, dim=1, eps=eps) # B, C
key = key.permute(1, 0) # C, B
key = F.normalize(key, p=2, dim=0, eps=eps)
similarity = torch.matmul(query, key) # B, B
assert similarity.max() < 1.001 and similarity.min() > -1.001, 'cosine similarity ranges [-1, 1]'
return similarity
input = torch.randn(16, 256, 8, 8)
print(sim(input, input).shape)
input = torch.randn(16, 256)
print(sim(input, input).shape)
用 SGD 或者 Adam 求解方程
SGD 解方程
def cal_dx(func,x,eps=1e-8):
d_func = func(x+eps) - func(x)
dx = d_func / eps
return dx
def solve(func,x,loss_func=lambda x:x**2, lr=0.001,num_iters=60000):
print('init x:', x)
for i in range(num_iters):
y = func(x)
d_loss_d_y = cal_dx(loss_func, y)
dy_dx = cal_dx(func, x)
grad_x = d_loss_d_y * dy_dx
x = x - grad_x*lr
return x
def check(func,x,eps=1e-8):
if abs(func(x)) < eps:
print('done')
else:
print('failed')
if __name__ == '__main__':
init = 7
func = lambda x: x**2+2*x-24
x = solve(func,init)
print(x)
check(func,x)
SGDm (把 solve 函数换一下)
def solve(func,x,loss_func=lambda x:x**2, lr=0.001,num_iters=60000, momentum=0.99):
print('init x:', x)
momentum_buf = None
for i in range(num_iters):
y = func(x)
d_loss_d_y = cal_dx(loss_func, y)
dy_dx = cal_dx(func, x)
grad_x = d_loss_d_y * dy_dx
if momentum_buf:
momentum_buf = momentum*momentum_buf + (1-momentum)*grad_x
else:
momentum_buf = grad_x
x = x - grad_x*lr
return x
BN (BatchNorm 在 train 和 test 的时候有什么不同)
import torch
from torch import nn
class BatchNorm(nn.Module):
# num_features:完全连接层的输出数量或卷积层的输出通道数。
# num_dims:2表示完全连接层,4表示卷积层
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 非模型参数的变量初始化为0和1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# 如果X不在内存上,将moving_mean和moving_var
# 复制到X所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.data
手写 MaxPooling / AvgPooling
import numpy as np
import torch
class MaxPooling2D:
def __init__(self, kernel_size=(2, 2), stride=2):
self.kernel_size = kernel_size
self.w_height = kernel_size[0]
self.w_width = kernel_size[1]
self.stride = stride
self.x = None
self.in_height = None
self.in_width = None
self.out_height = None
self.out_width = None
# 要记录下在当前的滑动窗中最大值的索引,反向求导要用到
self.arg_max = None
def __call__(self, x):
self.x = x
self.in_height = np.shape(x)[0]
self.in_width = np.shape(x)[1]
self.out_height = int((self.in_height - self.w_height) / self.stride) + 1
self.out_width = int((self.in_width - self.w_width) / self.stride) + 1
out = np.zeros((self.out_height, self.out_width))
self.arg_max = np.zeros_like(out, dtype=np.int32)
for i in range(self.out_height):
for j in range(self.out_width):
start_i = i * self.stride
start_j = j * self.stride
end_i = start_i + self.w_height
end_j = start_j + self.w_width
out[i, j] = np.max(x[start_i: end_i, start_j: end_j])
self.arg_max[i, j] = np.argmax(x[start_i: end_i, start_j: end_j])
self.arg_max = self.arg_max
return out
def backward(self, d_loss):
dx = np.zeros_like(self.x)
for i in range(self.out_height):
for j in range(self.out_width):
start_i = i * self.stride
start_j = j * self.stride
end_i = start_i + self.w_height
end_j = start_j + self.w_width
# 将索引展开成二维的
index = np.unravel_index(self.arg_max[i, j], self.kernel_size)
dx[start_i:end_i, start_j:end_j][index] = d_loss[i, j] #
return dx
class AvgPooling2D:
def __init__(self, kernel_size=(2, 2), stride=2):
self.stride = stride
self.kernel_size = kernel_size
self.w_height = kernel_size[0]
self.w_width = kernel_size[1]
def __call__(self, x):
self.x = x
self.in_height = x.shape[0]
self.in_width = x.shape[1]
self.out_height = int((self.in_height - self.w_height) / self.stride) + 1
self.out_width = int((self.in_width - self.w_width) / self.stride) + 1
out = np.zeros((self.out_height, self.out_width))
for i in range(self.out_height):
for j in range(self.out_width):
start_i = i * self.stride
start_j = j * self.stride
end_i = start_i + self.w_height
end_j = start_j + self.w_width
out[i, j] = np.mean(x[start_i: end_i, start_j: end_j])
return out
def backward(self, d_loss):
dx = np.zeros_like(self.x)
for i in range(self.out_height):
for j in range(self.out_width):
start_i = i * self.stride
start_j = j * self.stride
end_i = start_i + self.w_height
end_j = start_j + self.w_width
# 直接将 loss 均分给每一个像素点
dx[start_i: end_i, start_j: end_j] = d_loss[i, j] / (self.w_width * self.w_height)
return dx
np.set_printoptions(precision=4, suppress=True, linewidth=120)
x_numpy = np.random.random((1, 1, 6, 9))
x_tensor = torch.tensor(x_numpy, requires_grad=True)
max_pool_tensor = torch.nn.AvgPool2d((2, 2), 2)
max_pool_numpy = AvgPooling2D((2, 2), stride=2)
out_numpy = max_pool_numpy(x_numpy[0, 0])
out_tensor = max_pool_tensor(x_tensor)
d_loss_numpy = np.random.random(out_tensor.shape)
d_loss_tensor = torch.tensor(d_loss_numpy, requires_grad=True)
out_tensor.backward(d_loss_tensor)
dx_numpy = max_pool_numpy.backward(d_loss_numpy[0, 0])
dx_tensor = x_tensor.grad
# print('input \n', x_numpy)
print("out_numpy \n", out_numpy)
print("out_tensor \n", out_tensor.data.numpy())
print("dx_numpy \n", dx_numpy)
print("dx_tensor \n", dx_tensor.data.numpy())
参考了 https://www.jianshu.com/p/eac3dcfce1b1
手撸IOU计算公式
就是一个点,要记得加上 1 ,不然是错的!
def bb_intersection_over_union(boxA, boxB):
boxA = [int(x) for x in boxA]
boxB = [int(x) for x in boxB]
xA = max(boxA[0], boxB[0])
yA = max(boxA[1], boxB[1])
xB = min(boxA[2], boxB[2])
yB = min(boxA[3], boxB[3])
# 要加上 1 ,因为像素是一个点,并不是一个矩形
interArea = max(0, xB - xA + 1) * max(0, yB - yA + 1)
boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
iou = interArea / float(boxAArea + boxBArea - interArea)
return iou
一个 batch 的 box 计算 IOU:
def bbox_overlaps(bboxes1, bboxes2, mode='iou', is_aligned=False, eps=1e-6):
assert mode in ['iou', 'iof', 'giou'], f'Unsupported mode {mode}'
# Either the boxes are empty or the length of boxes' last dimension is 4
assert (bboxes1.size(-1) == 4 or bboxes1.size(0) == 0)
assert (bboxes2.size(-1) == 4 or bboxes2.size(0) == 0)
# Batch dim must be the same
# Batch dim: (B1, B2, ... Bn)
assert bboxes1.shape[:-2] == bboxes2.shape[:-2]
batch_shape = bboxes1.shape[:-2]
rows = bboxes1.size(-2)
cols = bboxes2.size(-2)
if is_aligned:
assert rows == cols
area1 = (bboxes1[..., 2] - bboxes1[..., 0]) * (
bboxes1[..., 3] - bboxes1[..., 1])
area2 = (bboxes2[..., 2] - bboxes2[..., 0]) * (
bboxes2[..., 3] - bboxes2[..., 1])
if is_aligned:
lt = torch.max(bboxes1[..., :2], bboxes2[..., :2]) # [B, rows, 2]
rb = torch.min(bboxes1[..., 2:], bboxes2[..., 2:]) # [B, rows, 2]
wh = fp16_clamp(rb - lt, min=0)
overlap = wh[..., 0] * wh[..., 1]
union = area1 + area2 - overlap
else:
lt = torch.max(bboxes1[..., :, None, :2],
bboxes2[..., None, :, :2]) # [B, rows, cols, 2]
rb = torch.min(bboxes1[..., :, None, 2:],
bboxes2[..., None, :, 2:]) # [B, rows, cols, 2]
wh = fp16_clamp(rb - lt, min=0)
overlap = wh[..., 0] * wh[..., 1]
union = area1[..., None] + area2[..., None, :] - overlap
eps = union.new_tensor([eps])
union = torch.max(union, eps)
ious = overlap / union
return ious
手撸 NMS (NMS 怎样实现的)
在目标检测中,常会利用非极大值抑制算法 (NMS) 对生成的大量候选框进行后处理 (post processing) ,去除冗余的候选框,得到最具代表性的结果,以加快目标检测的效率。一般是先得到生成的所有框,然后用一个参数 score_thr 筛除置信度太低的框,再将剩余框送入 nms 函数进行抑制,nms 一般有一个 iou_thr 参数,一般为 0.5。
NMS 算法的主要流程如下所示:
根据候选框的类别分类概率做排序:A<B<C<D<E<F
- 先标记最大概率矩形框 F 是我们要保留下来的;
- 从最大概率矩形框 F 开始,分别判断 A~E 与 F 的重叠度 IOU(两框的交并比)是否大于某个设定的阈值,假设 B、D 与 F 的重叠度超过阈值,那么就扔掉 B、D;
- 从剩下的矩形框 A、C、E 中,选择概率最大的 E,标记为要保留下来的,然后判读 E 与 A、C 的重叠度,扔掉重叠度超过设定阈值的矩形框
就这样一直重复下去,直到剩下的矩形框没有了,标记完所有要保留下来的矩形框
import numpy as np
def py_nms(dets, thresh):
"""Pure Python NMS baseline."""
#x1、y1、x2、y2、以及score赋值
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
scores = dets[:, 4]
#每一个候选框的面积
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
#order是按照score降序排序的
order = scores.argsort()[::-1]
keep = []
while order.size > 0:
i = order[0]
keep.append(i)
#计算当前概率最大矩形框与其他矩形框的相交框的坐标,会用到numpy的broadcast机制,得到的是向量
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
#计算相交框的面积,注意矩形框不相交时w或h算出来会是负数,用0代替
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
#计算重叠度IOU:重叠面积/(面积1+面积2-重叠面积)
ovr = inter / (areas[i] + areas[order[1:]] - inter)
#找到重叠度不高于阈值的矩形框索引
inds = np.where(ovr <= thresh)[0]
#将order序列更新,由于前面得到的矩形框索引要比矩形框在原order序列中的索引小1,所以要把这个1加回来
order = order[inds + 1]
return keep
# test
if __name__ == "__main__":
dets = np.array([[30, 20, 230, 200, 1],
[50, 50, 260, 220, 0.9],
[210, 30, 420, 5, 0.8],
[430, 280, 460, 360, 0.7]])
thresh = 0.35
keep_dets = py_nms(dets, thresh)
print(keep_dets)
print(dets[keep_dets])
手撸 CELoss、FocalLoss
主要是记住公式,尤其是 FocalLoss 的公式,前面是 (1-p),p 是经过 softmax 之后的概率,其实跟 CE 是一样的,如果 p 特别大的话 loss 就几乎是 0,然后用 gamma 进行指数运算,loss 就更小了,就是通过这样的机制来调整不同样本产生的 loss
# torch 版本
import torch
import torch.nn.functional as F
# => official
pred = torch.randn(5,5)
target = torch.tensor([0,3,1,2,4], dtype=torch.long)
official_ce_loss = F.cross_entropy(pred, target)
# => my
# softmax_logits = F.softmax(pred, dim=1) # 或者直接用这一句
softmax_logits = torch.exp(pred) / torch.sum(torch.exp(pred), dim=1)
onehot_target = F.one_hot(target)
my_ce_loss = -1 * torch.sum(onehot_target * torch.log(softmax_logits)) / pred.shape[0]
print(my_ce_loss)
print(official_ce_loss)
#focal
gamma = 2
alpha = 0.25
# => official
ce_loss = F.cross_entropy(pred, target,
reduction='none')
pt = torch.exp(-ce_loss)
official_focal_loss = (alpha * (1-pt) ** gamma * ce_loss).mean()
# => my
pt = F.softmax(pred, dim=1)
neg_ylogp = -1 * onehot_target * torch.log(pt)
focal = alpha * (1-pt) ** gamma * neg_ylogp
my_focal_loss = torch.sum(focal) / pred.shape[0]
print(my_focal_loss)
print(official_focal_loss)
reference:
https://github.com/kuaikuaikim/DFace/
https://blog.csdn.net/Blateyang/article/details/79113030
mmdet 中的 FocalLoss 写的太迷惑了,我把它改了一下贴上来,这样就符合了原来的公式了。 FocalLoss 要分正负样本去进行讨论。
def py_sigmoid_focal_loss(pred,
target,
weight=None,
gamma=2.0,
alpha=0.25,
reduction='mean',
avg_factor=None):
"""PyTorch version of `Focal Loss <https://arxiv.org/abs/1708.02002>`_.
Args:
pred (torch.Tensor): The prediction with shape (N, C), C is the
number of classes
target (torch.Tensor): The learning label of the prediction.
weight (torch.Tensor, optional): Sample-wise loss weight.
gamma (float, optional): The gamma for calculating the modulating
factor. Defaults to 2.0.
alpha (float, optional): A balanced form for Focal Loss.
Defaults to 0.25.
reduction (str, optional): The method used to reduce the loss into
a scalar. Defaults to 'mean'.
avg_factor (int, optional): Average factor that is used to average
the loss. Defaults to None.
"""
pred_sigmoid = pred.sigmoid()
target = target.type_as(pred)
# 改了一下
# 前面半部分计算了 target 为正样本时的 pt,后半部分对应了 target 为负样本时的 pt
pt = pred_sigmoid * target + (1 - pred_sigmoid) * (1 - target)
# 原论文中 focalloss 的系数,前面半部分是 target 为正样本时的 alpha,后半部分为负样本的 alpha
# 正样本和负样本的 alpha 系数为 1:3
focal_weight = (alpha * target + (1 - alpha) *
(1 - target)) * (1 - pt).pow(gamma)
# 下面是 mmdet 原版的 focalloss 系数,不直观,对新手不友好
# pt = (1 - pred_sigmoid) * target + pred_sigmoid * (1 - target)
# focal_weight = (alpha * target + (1 - alpha) *
# (1 - target)) * pt.pow(gamma)
loss = F.binary_cross_entropy_with_logits(
pred, target, reduction='none') * focal_weight
if weight is not None:
if weight.shape != loss.shape:
if weight.size(0) == loss.size(0):
# For most cases, weight is of shape (num_priors, ),
# which means it does not have the second axis num_class
weight = weight.view(-1, 1)
else:
# Sometimes, weight per anchor per class is also needed. e.g.
# in FSAF. But it may be flattened of shape
# (num_priors x num_class, ), while loss is still of shape
# (num_priors, num_class).
assert weight.numel() == loss.numel()
weight = weight.view(loss.size(0), -1)
assert weight.ndim == loss.ndim
loss = weight_reduce_loss(loss, weight, reduction, avg_factor)
return loss
另外 gaussian_focal_loss 用来计算 centernet 的 heatmap loss,也一起记录一下,老是会忘记。
@weighted_loss
def gaussian_focal_loss(pred: Tensor,
gaussian_target: Tensor,
alpha: float = 2.0,
gamma: float = 4.0,
pos_weight: float = 1.0,
neg_weight: float = 1.0) -> Tensor:
"""`Focal Loss <https://arxiv.org/abs/1708.02002>`_ for targets in gaussian
distribution.
Args:
pred (torch.Tensor): The prediction.
gaussian_target (torch.Tensor): The learning target of the prediction
in gaussian distribution.
alpha (float, optional): A balanced form for Focal Loss.
Defaults to 2.0.
gamma (float, optional): The gamma for calculating the modulating
factor. Defaults to 4.0.
pos_weight(float): Positive sample loss weight. Defaults to 1.0.
neg_weight(float): Negative sample loss weight. Defaults to 1.0.
"""
eps = 1e-12
# 正样本索引
pos_weights = gaussian_target.eq(1)
# 负样本索引
neg_weights = (1 - gaussian_target).pow(gamma)
# 正样本 loss,(1 - pred).pow(alpha) 为 focalloss 的系数,和原始的 focalloss 不一样
pos_loss = -(pred + eps).log() * (1 - pred).pow(alpha) * pos_weights
# 负样本 loss,pred.pow(alpha) 为 focalloss 的系数,因为是负样本
# pt = 1 - pred,公式中这里本来就是 1 - pt,所以变成了 pred
neg_loss = -(1 - pred + eps).log() * pred.pow(alpha) * neg_weights
return pos_weight * pos_loss + neg_weight * neg_loss
PyTorch api 实现 DCN
import torch
import torch.nn as nn
import torchvision.ops
class DeformableConv2d(nn.Module):
def __init__(self,
in_channels,
out_channels,
kernel_size=3,
stride=1,
padding=1,
bias=False):
super(DeformableConv2d, self).__init__()
assert type(kernel_size) == tuple or type(kernel_size) == int
kernel_size = kernel_size if type(kernel_size) == tuple else (kernel_size, kernel_size)
self.stride = stride if type(stride) == tuple else (stride, stride)
self.padding = padding
# 用这个卷积在每一个 feature 点上都预测出该点的采样 offset
# 相当于在某一点作为取样点时,卷积核的每一个 kernel 都需要在 x 和 y 方向产生偏移,
# 所以这个的通道是 2 * k * k
self.offset_conv = nn.Conv2d(in_channels,
2 * kernel_size[0] * kernel_size[1],
kernel_size=kernel_size,
stride=stride,
padding=self.padding,
bias=True)
# 论文里面说的把这卷积的权重给初始化成 0
nn.init.constant_(self.offset_conv.weight, 0.)
nn.init.constant_(self.offset_conv.bias, 0.)
# 这个是在 DCNv2 里面的对每一个采样点额外预测一个权重,防止采样到不需要的区域
self.modulator_conv = nn.Conv2d(in_channels,
1 * kernel_size[0] * kernel_size[1],
kernel_size=kernel_size,
stride=stride,
padding=self.padding,
bias=True)
# 权重初始化为 0.5
nn.init.constant_(self.modulator_conv.weight, 0.5)
nn.init.constant_(self.modulator_conv.bias, 0.)
# 这个就是正常的卷积,在后面的 deform_conv2d 接口中需要传入
self.regular_conv = nn.Conv2d(in_channels=in_channels,
out_channels=out_channels,
kernel_size=kernel_size,
stride=stride,
padding=self.padding,
bias=bias)
def forward(self, x):
# 得到采样的偏置
offset = self.offset_conv(x)
# 归一化到 (0,1) 作为采样的权重
modulator = torch.sigmoid(self.modulator_conv(x))
# 调用 torch 的 api,得到 DCN 之后的结果
# 其中 mask 参数为 None 的话则是 DCNv1, 传入上述 modulator 的话则是 DCNv2
# 低版本的 torch 不支持 DCNv2
x = torchvision.ops.deform_conv2d(input=x,
offset=offset,
weight=self.regular_conv.weight,
bias=self.regular_conv.bias,
padding=self.padding,
# mask=modulator,
stride=self.stride)
return x
dcn = DeformableConv2d(in_channels=3,
out_channels=128,
kernel_size=3)
input = torch.randn(4, 3, 224, 224)
out = dcn(input)
print(out.shape) # [4, 128, 224, 224]
手撸 MultiHeadAttention
import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F
class MultiHeadAttention(nn.Module):
'''
input:
query --- [N, T_q, query_dim]
key --- [N, T_k, key_dim]
mask --- [N, T_k]
T_q 相当于是图像中的 H*W
output:
out --- [N, T_q, embed_dim]
scores -- [h, N, T_q, T_k]
'''
def __init__(self, query_dim, key_dim, embed_dim, num_heads):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.key_dim = key_dim
self.W_query = nn.Linear(in_features=query_dim, out_features=embed_dim, bias=False)
self.W_key = nn.Linear(in_features=key_dim, out_features=embed_dim, bias=False)
self.W_value = nn.Linear(in_features=key_dim, out_features=embed_dim, bias=False)
def forward(self, query, key, mask=None):
querys = self.W_query(query) # [N, T_q, embed_dim]
keys = self.W_key(key) # [N, T_k, embed_dim]
values = self.W_value(key)
assert self.embed_dim % self.num_heads == 0
split_size = self.embed_dim // self.num_heads
querys = torch.stack(torch.split(querys, split_size, dim=2), dim=0) # [h, N, T_q, embed_dim/h]
keys = torch.stack(torch.split(keys, split_size, dim=2), dim=0) # [h, N, T_k, embed_dim/h]
values = torch.stack(torch.split(values, split_size, dim=2), dim=0) # [h, N, T_k, embed_dim/h]
## score = softmax(QK^T / (d_k ** 0.5))
scores = torch.matmul(querys, keys.transpose(2, 3)) # [h, N, T_q, T_k]
scores = scores / (self.key_dim ** 0.5)
## mask
if mask is not None:
## mask: [N, T_k] --> [h, N, T_q, T_k]
mask = mask.unsqueeze(1).unsqueeze(0).repeat(self.num_heads,1,querys.shape[2],1)
# 将 mask 中为 1 的元素所在的索引在 score 中替换成 -np.inf,经过 softmax 之后这部分的值会变成 0
# 相当于这部分就不进行 attention 的计算 ( np.exp(-np.inf) = 0 )
scores = scores.masked_fill(mask, -np.inf)
scores = F.softmax(scores, dim=3)
## out = score * V
out = torch.matmul(scores, values) # [h, N, T_q, embed_dim/h]
out = torch.cat(torch.split(out, 1, dim=0), dim=3).squeeze(0) # [N, T_q, embed_dim]
return out,scores
attention = MultiHeadAttention(256,512,256,16)
## 输入
qurry = torch.randn(8, 2, 256)
key = torch.randn(8, 6 ,512)
mask = torch.tensor([[False, False, False, False, True, True],
[False, False, False, True, True, True],
[False, False, False, False, True, True],
[False, False, False, True, True, True],
[False, False, False, False, True, True],
[False, False, False, True, True, True],
[False, False, False, False, True, True],
[False, False, False, True, True, True],])
## 输出
out, scores = attention(qurry, key, mask)
print('out:', out.shape) ## torch.Size([8, 2, 256])
print('scores:', scores.shape) ## torch.Size([16, 8, 2, 6])
双线性插值
在图像缩放中非常常用,本质就是用两次插值计算出非整数坐标的像素值。下面给出了逐像素的计算方法,很慢,维基百科里面有推导矩阵的形式,会更快。
ROI align 用到了双线性插值,记录一个讲得比较好的博客
https://zhuanlan.zhihu.com/p/73113289
import numpy as np
import cv2
from matplotlib import pyplot as plt
scale = 0.8
img_path = 'demo.jpg'
img = cv2.imread(img_path)
src_h = img.shape[0]
src_w = img.shape[1]
dst_h = int(scale*src_h) # 图像缩放倍数
dst_w = int(scale*src_w) # 图像缩放倍数
dst_img = np.zeros((dst_h, dst_w, 3), dtype=np.uint8)
import ipdb; ipdb.set_trace()
for c in range(3):
for h in range(dst_h):
for w in range(dst_w):
# 目标点在原图上的位置
# 使几何中心点重合
# src_x = (w+0.5)*src_w/dst_w-0.5
# src_y = (h+0.5)*src_h/dst_h-0.5
# 不考虑几何中心重合直接对应
src_x = w*src_w/dst_w
src_y = h*src_h/dst_h
if src_x<0:
src_x = 0
if src_y<0:
src_y = 0
# 确定最近的四个点
# np.floor()返回不大于输入参数的最大整数。(向下取整)
x1 = int(np.floor(src_x))
y1 = int(np.floor(src_y))
x2 = int(min(x1+1, src_w-1)) #防止超出原图像范围
y2 = int(min(y1+1, src_h-1))
# x方向线性插值,原公式本来要除一个(x2-x1),这里x2-x1=1
# 这里的 R1 R2 以及下面的 P 都是整数了
R1 = (x2-src_x)*img[y1,x1,c]+(src_x-x1)*img[y1,x2,c]
R2 = (x2-src_x)*img[y2,x1,c]+(src_x-x1)*img[y2,x2,c]
# y方向线性插值,同样,原公式本来要除一个(y2-y1),这里y2-y1=1
P = (y2-src_y)*R1+(src_y-y1)*R2
dst_img[h,w,c] = P
cv2.imwrite('bilinear_interped_img.jpg', dst_img)
🌟Leetcode 题目框架
通用排序算法
快排
class Solution {
int sort(vector<int>& nums,int left,int right)
{
int pivot=rand()%(right-left+1)+left;
int temp=nums[left];
nums[left]=nums[pivot];
nums[pivot]=temp;
pivot=nums[left];
while(left<right)
{
while(left<right&&nums[right]>=pivot)
right--;
nums[left]=nums[right];
while(left<right&&nums[left]<=pivot)
left++;
nums[right]=nums[left];
}
nums[left]=pivot;
return left;
}
void quick_sort(vector<int>& nums,int left,int right)
{
if(left>=right)
return;
int mid=sort(nums,left,right);
quick_sort(nums,left,mid-1);
quick_sort(nums,mid+1,right);
}
public:
vector<int> sortArray(vector<int>& nums) {
quick_sort(nums,0,nums.size()-1);
return nums;
}
};
归并
class Solution {
void merge(vector<int>& nums,int left,int right,vector<int>& ans)
{
int mid=(right-left)/2+left;
int i=left,j=mid+1,k=0;
while(i<=mid&&j<=right)
{
if(nums[i]<=nums[j])
ans[k++]=nums[i++];
else ans[k++]=nums[j++];
}
while(i<=mid)
{
ans[k++]=nums[i++];
}
while(j<=right)
ans[k++]=nums[j++];
for(int i=left;i<=right;i++)
nums[i]=ans[i-left];
}
void mergeSort(vector<int>& nums,int left,int right,vector<int>& ans)
{
if(left>=right)
return ;
int mid=(right-left)/2+left;
mergeSort(nums,left,mid,ans);
mergeSort(nums,mid+1,right,ans);
merge(nums,left,right,ans);
}
public:
vector<int> sortArray(vector<int>& nums) {
vector <int> ans(nums.size());
mergeSort(nums,0,nums.size()-1,ans);
return nums;
}
};
堆排
class Solution {
void head_down(int i,int size,vector<int>& nums)
{
while(i<size)
{
int left=2*i+1,right=2*i+2;
int max=i;
if(left<size&&nums[left]>nums[max])
max=left;
if(right<size&&nums[right]>nums[max])
max=right;
if(max==i)
break;
swap(nums[i],nums[max]);
i=max;
}
}
void maxHeapity(vector<int>& nums,int size)
{
for(int i=size/2-1;i>=0;i--)
head_down(i,size,nums);
}
public:
vector<int> sortArray(vector<int>& nums) {
int n=nums.size();
maxHeapity(nums,n);
swap(nums[0],nums[n-1]);
for(int i=n-2;i>0;i--)
{
n--;
head_down(0,n,nums);
swap(nums[0],nums[i]);
}
return nums;
}
};
二分框架(有序数组,找值或者左右边界)
class Solution {
public:
// 二分正确版本
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> res(2, -1);
if (!nums.size()) {
return res;
}
int left = begin(nums, target);
int right = end(nums, target);
res = {left, right};
return res;
}
int begin(vector<int> & nums, int target) {
int left = 0, right = nums.size() - 1;
while (left <= right) {
// 防止溢出
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
if (left >= nums.size() || nums[left] != target) {
return -1;
}
return left;
}
int end(vector<int> & nums, int target) {
int left = 0, right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
if (right < 0 || nums[right] != target) {
return -1;
}
return right;
}
};
滑动窗口框架
/* 滑动窗口算法框架 */
void slidingWindow(string s) {
unordered_map<char, int> window;
int left = 0, right = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
🌟Leetcode 链表专题
链表相交 (双指针)
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (!headA || !headB) {
return NULL;
}
ListNode * p1 = headA, * p2 = headB;
// 不相交的话最后都是 null, 也能跳出来
while (p1 != p2) {
p1 = p1 ? p1->next : headB;
p2 = p2 ? p2->next : headA;
}
return p1;
}
};
链表环 (双指针) (TODO)
合并 k 个有序链表 (优先队列,堆)
// 自定义一个比较函数传入优先队列的构造函数
class cmp1
{
public:
bool operator() (ListNode * a, ListNode * b)
{
// 小顶堆保证堆顶元素与其他元素比较时, < 一定是 false,所以这里是 >
return a->val > b->val;
}
};
class Solution
{
public:
ListNode* mergeKLists(vector<ListNode*>& lists)
{
if (lists.size() == 0)
return NULL;
// 优先队列的构造函数
priority_queue<ListNode *, vector<ListNode*>, cmp1> minHeap;
for (ListNode * x : lists)
{
if (x)
// 将存在值的链表 push 进小顶堆
minHeap.push(x);
}
ListNode * dummy = new ListNode(0);
ListNode * x = dummy;
while (!minHeap.empty())
{
// 找到堆中最小的值
ListNode * y = minHeap.top();
minHeap.pop();
// 更新结果链表
x->next = y;
x = x->next;
// 将这个链表下一个值再 push 进去进行排序
if (y->next)
{
minHeap.push(y->next);
}
}
return dummy->next;
}
};
环形链表2 (双指针判断交点)
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
if (!head) {
return NULL;
}
ListNode *fast = head, *slow = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
break;
}
}
if (!fast || !fast->next) {
// 无环
return NULL;
}
fast = head;
while (fast != slow) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};
K 个一组翻转链表
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if (!head) {
return nullptr;
}
ListNode *begin = head, *end = head;
for (int i = 0; i < k; i++) {
if (!end) return head;
end = end->next;
}
ListNode *reversed = reverse(begin, end);
// begin 现在成了翻转后链表的最后一个结点
begin->next = reverseKGroup(end, k);
return reversed;
}
// 反转 [A, B) 区间内的结点,注意是左闭右开,相当于把正常的函数签名由 null 改成了 B
ListNode *reverse(ListNode *A, ListNode *B) {
ListNode *pre = nullptr;
ListNode *cur = A;
ListNode *tmp = nullptr;
while (cur != B) { // 相当于把 A != nullptr 改成了 A != B
tmp = cur->next;
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
};
回文链表 🌟
给你一个单链表的头节点
head,请你判断该链表是否为回文链表。如果是,返回true;否则,返回false。思路:找中点,然后将后面一半反转,然后逐个对比
class Solution {
public:
bool isPalindrome(ListNode* head) {
if (!head) {
return true;
}
ListNode * left_end = find_middle(head);
ListNode * right_begin = left_end->next;
ListNode * right_reverse = reverse(right_begin);
left_end->next = nullptr;
// 左边可能比右边多一个元素 (链表为单数)
while (right_reverse) {
if (right_reverse->val != head->val) {
return false;
}
head = head->next;
right_reverse = right_reverse->next;
}
return true;
}
ListNode* find_middle(ListNode * node) {
if (!node) {
return nullptr;
}
ListNode * fast = node, * slow = node;
while (fast->next && fast->next->next) {
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
ListNode* reverse(ListNode * node) {
ListNode * pre = nullptr, * cur = node;
while (cur) {
ListNode * t = cur->next;
cur->next = pre;
pre = cur;
cur = t;
}
return pre;
}
};
🌟 Leetcode 堆专题
数组中第 k 大的数
给定整数数组
nums和整数k,请返回数组中第k个最大的元素。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
// 将所有元素过一遍小顶堆
priority_queue<int, vector<int>, greater<int> > q;
for (auto & num: nums) {
q.push(num);
// 如果数量大于 k 就 pop 堆顶元素
if (q.size() > k) {
q.pop();
}
}
// 留下来的就是最大的 k 个元素,堆顶就是第 k 大元素
return q.top();
}
};
🌟 Leetcode 动规专题
最长公共子序列 (动规)
// string 类题目就用两个指针指向两个 string,一边移动,动态规划题目
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int l1 = text1.size();
int l2 = text2.size();
// 定义:s1[0..i-1] 和 s2[0..j-1] 的 lcs 长度为 dp[i][j]
vector<vector<int>> dp(l1+1, vector<int>(l2+1, 0));
for (int i = 1; i <= l1; i++) {
for (int j = 1; j <= l2; j++) {
if (text1[i-1] == text2[j-1]) {
dp[i][j] = 1 + dp[i-1][j-1];
} else {
dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
}
}
}
return dp[l1][l2];
}
};
最长回文子序列 (动规)
// 更绝的做法是将 s 反转,求他们的最长公共子序列就是答案
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
// dp 数组全部初始化为 0
// dp[i][j] 代表了 s[i,j] 的最长回文子串
vector<vector<int>> dp(n, vector<int>(n, 0));
// base case,i 和 j 相等的话回文串长度就是 1,也就是自己
// 并且 i > j 的地方,长度为 0,已经被初始化了
for (int i = 0; i < n; i++)
dp[i][i] = 1;
// 反着遍历保证正确的状态转移
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
// 状态转移方程
if (s[i] == s[j])
dp[i][j] = dp[i + 1][j - 1] + 2;
else
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
// 整个 s 的最长回文子串长度
return dp[0][n - 1];
}
};
最长递增子序列 (动规)
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> dp(nums.size(), 1);
// 对每一个数字来说
// dp[i] 代表了以它结尾的最长序列长度
// 计算的逻辑就是前面以比他的值小的数为结尾的最长序列长度 + 1,由于可能有很多个,所以取最大值
for (int i = 0; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
// 找到最大的序列
int res = 0;
for (int i = 0; i < dp.size(); i++) {
if (dp[i] > res) {
res = dp[i];
}
}
return res;
}
};
爬楼梯 /斐波那契 (动规)
//假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
//每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n+1);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
// 爬到第n阶的种数=爬到n-1阶的种数+爬到n-2阶的种数
// 因为两种情况下都只用再爬1次或者2次
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
};
零钱兑换 (动规)
// 动态规划,凑 amount 需要的硬币数等于凑 amount -coin 需要的硬币数 + 1
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
// 不能初始化为 INT_MAX,否则会越界
vector<int> dp(amount + 1, amount + 1);
// base case
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int c: coins) {
// < 0 的话这种面值就不行
if (i - c < 0) {
continue;
} else {
dp[i] = min(dp[i], dp[i - c] + 1);
}
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}
};
零钱兑换 II (背包动规)
class Solution {
public:
int change(int amount, vector<int>& coins) {
// 定义 DP table
int size = coins.size();
// DP table 的定义:若只使用前 i 个物品(可以重复使用),当背包容量为 j 时,有 dp[i][j] 种方法可以装满背包
vector<vector<int>> dp(size+1, vector<int>(amount+1, 0));
// 容量为 0,只有一种(什么都不装)
for (int i = 0; i <= size; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= size; i++) {
for (int j = 1; j <= amount; j++) {
// 背包容量不足,不足以使用第 i 个硬币
if (j-coins[i-1] < 0) {
dp[i][j] = dp[i-1][j];
} else {
// 将低第 i 个数放不放进背包
// dp[i][j-coins[i-1]] 也就代表放进背包,意思就是已知第 i 个硬币的面值
// 使用前 i -1 种硬币能凑出总额减去自己面额的组合数,但是这里硬币无限用
// 所以反映到 dp 方程上就是 i 而不是 i-1
dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]];
}
}
}
return dp[size][amount];
}
};
丑数 (动规 + 三指针)
// 由于丑数只含有 2、3、5,所以对于第 n+1 个丑数一定是来自前 n 个丑数中某一个乘以 2 或 3 或 5 得到的
class Solution {
public:
int nthUglyNumber(int n) {
int n_2 = 0, n_3 = 0, n_5 = 0;
vector<int> dp(n);
dp[0] = 1;
for (int i = 1; i < n; i++) {
int s_2 = dp[n_2]*2;
int s_3 = dp[n_3]*3;
int s_5 = dp[n_5]*5;
dp[i] = min(min(s_2, s_3), s_5);
// 不能用 if else,因为一个丑数可能同时满足多个条件
if (dp[i] == s_2) n_2++;
if (dp[i] == s_3) n_3++;
if (dp[i] == s_5) n_5++;
}
return dp[n-1];
}
};
分割等和子集 (背包动规)
// 转化成背包问题来做,数字能否填满 sum/2 容量的背包
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for (int i : nums) sum += i;
// 为奇数的话不能分割
if (sum % 2) return false;
int target = sum / 2;
// 定义 DP table
int size = nums.size();
// DP table 的定义:dp[i][j]->对于前i个物体,当背包的容量为j时,能不能装满
vector<vector<int>> dp(size+1, vector<int>(target+1, false));
for (int i = 0; i <= size; i++) {
dp[i][0] = true;
}
for (int j = 0; j <= target; j++) {
dp[0][j] = false;
}
for (int i = 1; i <= size; i++) {
for (int j = 1; j <= target; j++) {
// 背包容量不足,不足以放进第 i 个物体
if (j-nums[i-1] < 0) {
dp[i][j] = dp[i-1][j];
} else {
// 将低第 i 个数放不放进背包
dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
}
}
}
return dp[size][target];
}
};
最小路径和 (动规)
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int r = grid.size();
int c = grid[0].size();
vector<vector<int> > dp(r, vector<int>(c, 0));
dp[0][0] = grid[0][0];
for (int i = 1; i < r; i++) {
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for (int i = 1; i < c; i++) {
dp[0][i] = dp[0][i-1] + grid[0][i];
}
for (int i = 1; i < r; i++) {
for (int j = 1; j < c; j++) {
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
}
}
return dp[r-1][c-1];
}
};
最大正方形 (动规)
在一个由
'0'和'1'组成的二维矩阵内,找到只包含'1'的最大正方形,并返回其面积。
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
// dp[i][j] 为以 matrix[i][j] 为右下角元素的全为 1 正方形矩阵的最大边长
int r = matrix.size(), c = matrix[0].size();
vector<vector<int> > dp(r, vector<int>(c, 0));
// 边缘的 case
for (int i = 0; i < r; i++) {
dp[i][0] = (matrix[i][0] == '1' ? 1 : 0);
}
for (int i = 0; i < c; i++) {
dp[0][i] = (matrix[0][i] == '1' ? 1 : 0);
}
for (int i = 1; i < r; i++) {
for (int j = 1; j < c; j++) {
// 如果是 0 的话不可能是正方形的右下角
if (matrix[i][j] == '0') {
continue;
}
// 状态转移,边长为左上角,左边,上边的正方形的最小边长加上自己的 (也就是 1)
dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
}
}
// 排序
int res = 0;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
res = max(res, dp[i][j]);
}
}
return res*res;
}
};
最大子数组和 (动规)
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int len = nums.size();
vector<int> dp(len, 0);
// 以 nums[i] 为结尾的「最大子数组和」为 dp[i]
// dp[i] 有两种「选择」,要么与前面的相邻子数组连接,形成一个和更大的子数组;
// 要么不与前面的子数组连接,自成一派,自己作为一个子数组。
dp[0] = nums[0];
for (int i = 1; i < len; i++) {
dp[i] = max( dp[i-1]+nums[i], nums[i] );
}
int res = INT_MIN;
for (auto & v : dp) {
if (v > res) {
res = v;
}
}
return res;
}
// 优化版本,因为 dp 方程只与上一次 dp 有关,所以可以不用数组,用一个值变化就行了
int maxSubArray(vector<int>& nums) {
int len = nums.size();
if (!len) {
return 0;
}
int dp = nums[0];
int res = dp; // 不能为 INT_MIN,如果数组只有一个值的话进不去下面的循环会返回 INT_MIN 作为答案
// 以 nums[i] 为结尾的「最大子数组和」为 dp[i]
// dp[i] 有两种「选择」,要么与前面的相邻子数组连接,形成一个和更大的子数组;
// 要么不与前面的子数组连接,自成一派,自己作为一个子数组。
for (int i = 1; i < len; i++) {
dp = max( nums[i], nums[i]+dp );
// 顺便做一个比较,就不用重复遍历所有值了
res = max(res, dp);
}
return res;
}
};
🌟 Leetcode 二叉树专题
二叉树层序遍历
class Solution {
private:
vector<vector<int>> res;
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (!root) {
return res;
}
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int size = q.size();
vector<int> vec;
for (int i = 0; i < size; i++) {
TreeNode* cur = q.front();
q.pop();
vec.push_back(cur->val);
if (cur->left) q.push(cur->left);
if (cur->right) q.push(cur->right);
}
res.push_back(vec);
}
return res;
}
};
二叉树的后序遍历序列
https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/
class Solution {
public:
// 牛逼,如果这是后序遍历序列的话,那么序列就是 左 右 中
// 最后一个一定是根结点,遍历序列找到第一个大于根结点的元素,左边一定是左子树
// 遍历右子树,如果所有值都是大于根结点的话,这是后序遍历序列
// 递归左右子树,重复上述步骤,如果只剩一个结点的话,返回True
bool verifyPostorder(vector<int>& postorder) {
// 遍历的起始与终结点
return recurverify(postorder, 0, postorder.size()-1);
}
bool recurverify(const vector<int>& arr, int left, int right){
// 注意这个边界条件,说明只有一个结点或者没有结点
if(left >= right) return true;
int target = left;
int root = arr[right];
while(arr[target] < root) target++;
// 右子树的起始点
int mid = target;
for (int i = mid; i < right; i++) {
if (arr[i] < root) {
return false; // 右子树一定大于根节点
}
}
return recurverify(arr, left, mid-1) && recurverify(arr, mid, right -1);
}
};
##
二叉树中和为某一值的路径
https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/
class Solution {
public:
vector<vector<int>> res;
vector<int> track;
int sum = 0;
vector<vector<int>> pathSum(TreeNode* root, int target) {
if (!root) {
return res;
}
// 先将根结点放进去
// 不然放到函数里的话比较难搞
sum += root->val;
track.push_back(root->val);
bt(root, target);
return res;
}
void bt(TreeNode* node, int target) {
// 叶子结点
if (!node->left && !node->right) {
if (sum == target) {
res.push_back(track);
}
return;
}
if (node->left) {
track.push_back(node->left->val);
sum += node->left->val;
bt(node->left, target);
track.pop_back();
sum -= node->left->val;
}
if (node->right) {
track.push_back(node->right->val);
sum += node->right->val;
bt(node->right, target);
track.pop_back();
sum -= node->right->val;
}
}
};
树的子结构
https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
// 有一个空的话就不符合
if (!A || !B) {
return false;
}
// 不是 A 的子结构就去 A 的子树中继续判断
if (judge(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B)) {
return true;
}
return false;
}
bool judge(TreeNode *A, TreeNode *B) {
// base case
if (!B) return true; // B 空的话说明被匹配完了
if (!A) return false; // A 空的话说明 B 还没匹配完,所以不包含子树
if (A->val != B->val) return false;
return judge(A->left, B->left) && judge(A->right, B->right);
}
};
二叉树展开为链表
// 跳出递归调用,只在意递归本身的作用
// flatten 可以将树展开成链表,我们只需要知道这个功能以及这种递归的 base case 就可以了
// 不用关心递归栈是怎么调用的
class Solution {
public:
void flatten(TreeNode* root) {
// base case
if (!root) return;
// 递归调用
flatten(root->left);
flatten(root->right);
// 此时左右子树已经被展开成链表了
TreeNode *linked_list_left = root->left;
TreeNode *linked_list_right = root->right;
// 清空左边的节点(很重要)
root->left = nullptr;
// 将左边的链表挂上根节点
root->right = linked_list_left;
TreeNode *tmp = root;
// 遍历到尽头
while (tmp->right) {
tmp = tmp->right;
}
// 将原来的右链表挂上去
tmp->right = linked_list_right;
}
};
二叉树中的最大路径和
一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。路径和 是路径中各节点值的总和。给你一个二叉树的根节点 root ,返回其 最大路径和 。
class Solution {
public:
int res = INT_MIN; // 防止节点的值全是负数
int maxPathSum(TreeNode* root) {
// 用递归后序遍历的思想,计算 root 的左右子树的最大和
// base case
if (!root) {
return 0;
}
singleSideMax(root);
return res;
}
// 辅助函数,计算以 root 为起点的最大单边路径和
int singleSideMax(TreeNode * root) {
// base case
if (!root) {
return 0;
}
// 左右子树的单边路径最大值
// 如果是负数的话不如直接不取,所以用 max 进行过滤
int left_max = max(0, singleSideMax(root->left));
int right_max = max(0, singleSideMax(root->right));
// 顺便更新一下结果
int sum_max = root->val + left_max + right_max;
res = max(res, sum_max);
return max(left_max, right_max) + root->val;
}
};
二叉树的最近公共祖先
// 分情况讨论,两个节点都在 root 子树,只有一个在,两个都不在
// 建议看题解 k 哥的图文详解
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// base case
if (!root || root == p || root == q) {
return root;
}
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if (!left && !right) {
return nullptr;
}
if (left && right) {
return root;
}
return left ? left : right;
}
};
🌟 Leetcode 图专题
判断二分图 (DFS 涂色 / 并查集)
// 用涂色法判定二分图
// DFS 版本递归
class Solution {
private:
bool res = true;
public:
bool isBipartite(vector<vector<int>>& graph) {
int num_nodes = graph.size();
vector<bool> visited(num_nodes, false);
vector<bool> color(num_nodes, false);
for (int i = 0; i < num_nodes; i++) {
if (!visited[i]) { // 如果该节点没被涂色遍历涂色
traverse(graph, i, visited, color);
}
}
return res;
}
void traverse(vector<vector<int>> & graph, int nodeVal, vector<bool> & visited, vector<bool> & color) {
if (!res) {
return;
}
visited[nodeVal] = true; // 对该节点涂色
for (int i = 0; i < graph[nodeVal].size(); i++) { // 遍历该节点的邻居节点
int neighbor = graph[nodeVal][i];
if (!visited[neighbor]) { // 如果没有涂色就将邻居涂成不一样的颜色
color[neighbor] = !color[nodeVal];
traverse(graph, neighbor, visited, color);
} else {
// 如果已经访问过邻居节点的话就判断邻居和自己的颜色是不是一样的
if (color[neighbor] == color[nodeVal]) {
res = false;
}
}
}
}
};
// 并查集主要就是三个函数,union,find,conncted
class UnionFind {
private:
int count;
vector<int> parent;
public:
UnionFind(int n) {
count = n;
parent.resize(n); // 预留好这么多长度,不然会报错
for (int i = 0; i < n; i++) {
parent[i] = i; // 自己的根结点就是自己
}
}
void union_(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (qRoot == pRoot) {
return;
}
parent[qRoot] = pRoot; // 将两个联通域合并
count--; // 连通域减少一个
}
int find(int v) {
while (parent[v] != v) {
// 进行路径压缩,防止某个联通域太长造成极端时间复杂度(退化成链表)
parent[v] = find(parent[v]); // 相比不压缩的并查集就只是多了这一行
}
return v;
}
bool connected(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
return pRoot == qRoot;
}
};
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
UnionFind* uf = new UnionFind(26);
for (auto & s: equations) {
// 把相等的元素进行连通
// 这里用字符操作将字符转化成 int 型整数
if (s[1] == '=') {
int a = s[0] - 'a';
int b = s[3] - 'a';
uf->union_(a, b);
}
}
for (auto & s: equations) {
// 然后判断不相等的
// 如果不想等的两个元素连通的话与上面违背了,所以返回 false
if (s[1] == '!') {
int a = s[0] - 'a';
int b = s[3] - 'a';
if (uf->connected(a, b)) {
return false;
}
}
}
return true;
}
};
🌟 Leetcode 二进制专题
只出现一次的数字
class Solution {
public:
int singleNumber(vector<int>& nums) {
// 位运算版本,真他妈妙
int res = 0;
// 数字最多不超过 32 位
for (int i = 0; i < 32; i++) {
int single_total = 0;
for (int val: nums) {
// 取出来每一位的值 (0 或者 1)
single_total += (val >> i) & 1;
}
// 3 个相同的数每一位加起来一定是 3 的倍数
// 如果有余数的话就是 res 上的数
if (single_total % 3) {
// 将结果放到相应的位上
res |= (1 << i);
}
}
return res;
}
};
二进制加法
# 直接模拟法
class Solution:
def addBinary(self, a: str, b: str) -> str:
if len(a) > len(b):
b = '0' * (len(a) - len(b)) + b
elif len(a) < len(b):
a = '0' * (len(b) - len(a)) + a
res = [x for x in '0' * (len(b) + 1)]
a = [x for x in a]
b = [x for x in b]
carry = 0
for i in range(len(b)):
val_b = int(b[-1 - i])
val_a = int(a[-1 - i])
sum = val_a + val_b + carry
if sum == 0:
carry = 0
res[-1 - i] = '0'
elif sum == 1:
carry = 0
res[-1 - i] = '1'
elif sum == 2:
carry = 1
res[-1 - i] = '0'
elif sum == 3:
carry = 1
res[-1 - i] = '1'
if carry:
res[0] = '1'
else:
res = res[1:]
return ''.join(res)
🌟 Leetcode 双指针专题
排序数组的两数之和
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int left = 0, right = numbers.size() - 1;
while (left < right) {
if (numbers[left] + numbers[right] > target) {
right--;
} else if (numbers[left] + numbers[right] < target) {
left++;
} else {
vector<int> res(2);
res = {left, right};
return res;
}
}
return vector<int>();
}
};
搜索旋转排序数组 (二分法)
整数数组 nums 按升序排列,数组中的值 互不相同 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。 你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
class Solution {
public:
// 旋转后一定有一边是有序的,用二分不断查找
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
}
// 右边有序
else if (nums[mid] <= nums[right]) {
// target 在有序的一边
if (nums[mid] < target && nums[right] >= target) {
left = mid + 1;
}
// target 在另外一边
else {
right = mid - 1;
}
}
// 左边有序
else if (nums[mid] > nums[right]) {
// target 在有序的一边
if (nums[left] <= target && nums[mid] > target) {
right = mid -1;
}
// target 在另外一边
else {
left = mid + 1;
}
}
}
return -1;
}
};
🌟 Leetcode 区间专题
合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int> > res;
if (!intervals.size()) {
return res;
}
// 先按照区间的开始来进行排序
sort(intervals.begin(), intervals.end());
// 先初始化最左端的值
int l = intervals[0][0], r = intervals[0][1];
for (int i = 1; i < intervals.size(); i++) {
// 如果下一段区间的开始在上一段的结束之后就是一段新的区间
if (intervals[i][0] > r) {
res.push_back({l, r});
l = intervals[i][0];
r = intervals[i][1];
} else {
// 否则就对两个区间进行合并
// 注意要用 max,因为下一段区间的结束时间不一定比上一段长
r = max(r, intervals[i][1]);
}
}
res.push_back({l, r});
return res;
}
};
插入区间
给你一个 无重叠的 ,按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
class Solution {
public:
vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
vector<vector<int> > res;
if (!intervals.size()) {
res.push_back(newInterval);
return res;
}
// 三种情况按照顺序分别讨论(画个模拟图就知道了)
// 当前区间和新的不重叠,并且处于新区间的左边,那么直接 push 进结果
int idx = 0;
int n = intervals.size();
while (idx < n && intervals[idx][1] < newInterval[0]) {
res.push_back(intervals[idx]);
idx++;
}
// 当前区间和新的重叠,那么进行合并
while (idx < n && intervals[idx][0] <= newInterval[1]) {
// 循环更新左右边界,直到没有重叠了
newInterval[0] = min(intervals[idx][0], newInterval[0]);
newInterval[1] = max(intervals[idx][1], newInterval[1]);
idx++;
}
res.push_back(newInterval);
// 当前区间和新的不重叠,并且处于新区间的右边,那么直接 push 进结果
while (idx < n && intervals[idx][0] > newInterval[1]) {
res.push_back(intervals[idx]);
idx++;
}
return res;
}
};
删除被覆盖区间
给你一个区间列表,请你删除列表中被其他区间所覆盖的区间。
只有当 c <= a 且 b <= d 时,我们才认为区间 [a,b) 被区间 [c,d) 覆盖。
在完成所有删除操作后,请你返回列表中剩余区间的数目。
class Solution {
public:
int removeCoveredIntervals(vector<vector<int>>& intervals) {
int res = intervals.size();
// 直接排序然后判断一下结束的时间就行了,画个草图就明白
// 排序要按找开始的顺序排,相同的话则让结束时间更大的排在前面
sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b)
{
if (a[0] == b[0]) {
return a[1] > b[1];
} else {
return a[0] < b[0];
}
});
int last = 0;
for (int i = 1; i < intervals.size(); i++) {
// 上一个区间的结束比这个区间早,没有被包围,更新结果
if (intervals[last][1] < intervals[i][1]) {
last = i;
} else {
res--;
}
}
return res;
}
};
🌟 Leetcode 回溯&DFS专题
集合(元素不重,不可复选)
给你一个整数数组
nums,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
class Solution {
public:
vector<int> track;
vector<vector<int> > res;
vector<vector<int>> subsets(vector<int>& nums) {
bt(nums, 0);
return res;
}
void bt(vector<int> & nums, int start) {
res.emplace_back(track);
// base case
if (start == nums.size()) {
return;
}
for (int i = start; i < nums.size(); i++) {
track.emplace_back(nums[i]);
bt(nums, i+1);
track.pop_back();
}
}
};
组合(元素不重,不可复选)
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
class Solution {
public:
vector<vector<int> > res;
vector<int> track;
vector<vector<int>> combine(int n, int k) {
bt(n, k, 1);
return res;
}
void bt(int n, int k, int start) {
if (track.size() == k) {
res.emplace_back(track);
return;
}
for (int i = start; i <= n; i++) {
track.emplace_back(i);
bt(n, k, i+1);
track.pop_back();
}
}
};
排列(元素不重,不可复选)
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
class Solution {
public:
vector<vector<int> > res;
vector<int> track;
unordered_map<int, int> umap;
vector<vector<int>> permute(vector<int>& nums) {
bt(nums);
return res;
}
void bt(vector<int> & nums) {
// base case
if (track.size() == nums.size()) {
res.emplace_back(track);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (umap[i]) {
continue;
}
umap[i]++;
track.emplace_back(nums[i]);
bt(nums);
umap[i]--;
track.pop_back();
}
}
};
集合(元素可重,不可复选)
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
class Solution {
public:
vector<vector<int> > res;
vector<int> track;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
// 有重复的话就先排序
sort(nums.begin(), nums.end());
bt(nums, 0);
return res;
}
void bt(vector<int> & nums, int start) {
res.emplace_back(track);
if (start == nums.size()) {
return;
}
// base case
for (int i = start; i < nums.size(); i++) {
// 剪枝
if (i > start && nums[i-1] == nums[i]) {
continue;
}
track.emplace_back(nums[i]);
bt(nums, i+1);
track.pop_back();
}
}
};
组合(元素可重,不可复选)
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
class Solution {
public:
vector<vector<int> > res;
vector<int> track;
int sum = 0;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
// 有重复的先排序
sort(candidates.begin(), candidates.end());
bt(candidates, 0, target);
return res;
}
void bt(vector<int> & nums, int start, int target) {
// base case
if (sum == target) {
res.emplace_back(track);
return;
}
// 不加后面这个 sum 和 target 的判断的话会超时
if (start == nums.size() || sum > target) {
return;
}
for (int i = start; i < nums.size(); i++) {
// 剪枝去重
if (i > start && nums[i] == nums[i-1]) {
continue;
}
track.emplace_back(nums[i]);
sum += nums[i];
bt(nums, i+1, target);
track.pop_back();
sum -= nums[i];
}
}
};
排列(元素可重,不可复选)
给定一个可包含重复数字的序列
nums,按任意顺序 返回所有不重复的全排列。
class Solution {
public:
vector<vector<int> > res;
vector<int> track;
unordered_map<int, int> umap;
vector<vector<int>> permuteUnique(vector<int>& nums) {
//有重复先排序
sort(nums.begin(), nums.end());
bt(nums);
return res;
}
void bt(vector<int> & nums) {
// base case
if (track.size() == nums.size()) {
res.emplace_back(track);
}
for (int i = 0; i < nums.size(); i++) {
if (umap[i]) {
continue;
}
// 剪枝策略
if (i > 0 && nums[i] == nums[i-1] && umap[i-1]) {
continue;
}
umap[i]++;
track.emplace_back(nums[i]);
bt(nums);
umap[i]--;
track.pop_back();
}
}
};
组合(元素不重,可复选)
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
class Solution {
public:
vector<vector<int> > res;
vector<int> track;
int sum = 0;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
bt(candidates, 0, target);
return res;
}
void bt(vector<int> & nums, int start, int target) {
// base case
if (sum == target) {
res.emplace_back(track);
return;
}
if (sum > target) {
return;
}
for (int i = start; i < nums.size(); i++) {
sum += nums[i];
track.emplace_back(nums[i]);
// 可以重复取的话就直接从 i 继续回溯,不用 i+1
bt(nums, i, target);
sum -= nums[i];
track.pop_back();
}
}
};
矩阵中的路径
https://leetcode.cn/problems/ju-zhen-zhong-de-lu-jing-lcof/
class Solution {
public:
map< pair<int, int>, int> used;
bool exist(vector<vector<char>>& board, string word) {
// 路径的开头可以是任意一个位置,不一定是 (0,0)
// 直接记录对应 index 的值,不等的话就是 false,进行剪枝
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
if (bt(board, word, i, j, 0)) {
return true;
}
}
}
return false;
}
bool bt(vector<vector<char>>& board, string word, int i, int j, int cur_idx) {
if (i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || board[i][j] != word[cur_idx]) {
return false;
}
if (used[make_pair(i, j)]) {
return false;
}
// base case
if (cur_idx == word.size()-1){
return true;
}
used[make_pair(i, j)]++;
bool res = bt(board, word, i-1, j, cur_idx+1)
|| bt(board, word, i+1, j, cur_idx+1)
|| bt(board, word, i, j-1, cur_idx+1)
|| bt(board, word, i, j+1, cur_idx+1);
used[make_pair(i, j)]--;
return res;
}
};
机器人的运动范围 (DFS)
https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof
class Solution {
public:
int movingCount(int m, int n, int k) {
int res = 0;
vector<vector<int> > used(m, vector<int> (n, 0));
res = dfs(0, 0, m, n, k, used);
return res;
}
// dfs 题,和回溯不一样,回溯需要取消,这个不用取消,找到一个答案就行了
// 要传入引用,不然结果会错
int dfs(int i, int j, int r, int c, int k, vector<vector<int> >& used) {
int sum = i % 10 + i / 10 % 10 + i / 100 % 10 + j % 10 + j / 10 % 10 + j / 100 % 10;
// base case
if (i < 0 || i >= r || j < 0|| j >= c || sum > k) {
return 0;
}
// 走过就不能再走
if (used[i][j]) {
return 0;
}
used[i][j]++;
return 1 + dfs(i+1, j, r, c, k, used)
+ dfs(i-1, j, r, c, k, used)
+ dfs(i, j-1, r, c, k, used)
+ dfs(i, j+1, r, c, k, used);
}
};
🌟 Leetcode 经典问题系列
股票问题
int maxProfit(vector<int>& prices) {
// 股票问题,三层 dp
// dp[i][k][0/1] 表示第i天,最多进行k次交易时,持有或者不持有股票的最大利润
// 状态转移方程(最后一维表示持有或者不持有股票):
// dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
// dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
int k_max = 2;
vector<vector<vector<int>>> dp(prices.size(), vector<vector<int>>(k_max+1, vector<int>(2)));
for (int i = 0; i < prices.size(); i++) {
// 穷举所有 k
for (int k = 1; k <= k_max; k++) {
if (i == 0) {
// base case
// dp[-1][0] = 0, dp[-1][1] = -inf
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue; // continue 不要忘记加
}
// 今天不持有股票,利润=max(休息,卖掉)
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1]+prices[i]);
// 今天持有股票,利润=max(休息,买入)
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0]-prices[i]);
}
}
// 最后一天肯定是把股票卖出去的利润大于不买的利润
return dp[prices.size()-1][k_max][0];
}
打家劫舍问题
如果是连续的数组或者环形数组的话可以直接套用股票的模版,如果是二叉树的话可以套用自上到下动规
// 首尾不能同时偷,所以有三种情况,只偷首,只偷尾,首位都不偷
// 第三种情况的收益没有前两种大,所以只判断两种就行了
int rob(vector<int>& nums) {
if (!nums.size()) {
return 0;
}
if (nums.size() == 1) {
return nums[0];
}
// 两种情况取最大值
return max(rob_between(nums, 0, nums.size()-1), rob_between(nums, 1, nums.size()));
}
// 打家劫舍第一题的做法
int rob_between(vector<int>& nums, int begin, int end) {
vector<vector<int>> dp(nums.size(), vector<int>(2));
for (int i = begin; i < end; i++) {
if (i == begin) {
dp[i][0] = 0;
dp[i][1] = nums[i];
continue;
}
dp[i][0] = max(dp[i-1][0], dp[i-1][1]);
dp[i][1] = max(dp[i-1][0]+nums[i], dp[i-1][1]);
}
cout << dp[end-1][0];
return max(dp[end-1][0], dp[end-1][1]);
}
unordered_map<TreeNode*, int> memo;
int rob(TreeNode* root) {
if (!root) {
return 0;
}
// 备忘录消除重叠子问题
if (memo.find(root) != memo.end()) {
return memo[root];
}
// 抢
int do_it = root->val
+ (root->left ? rob(root->left->left)+rob(root->left->right): 0)
+ (root->right ? rob(root->right->left)+rob(root->right->right): 0);
// 不抢
int not_do = rob(root->left)+rob(root->right);
int res = max(do_it, not_do);
memo[root] = res;
return res;
}
接雨水问题
class Solution {
public:
// 双指针
int trap(vector<int>& height) {
int res = 0;
int left = 0, right = height.size()-1;
// 初始化当前左边区域最大的高,右边区域最大的高
int l_max = 0, r_max = 0;
while (left < right) {
l_max = max(l_max, height[left]);
r_max = max(r_max, height[right]);
if (l_max < r_max) {
res += l_max - height[left];
left++;
} else {
res += r_max - height[right];
right--;
}
}
return res;
}
};
约瑟夫环
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
class Solution {
public:
int lastRemaining(int n, int m) {
int res = 0;
// 只有一个数字的话,也即是 i==1 情况,留下的一定是 0
for (int i = 2; i <= n; i++) {
res = (res + m) % i;
}
return res;
}
};
封闭岛屿的数量
class Solution {
public:
int closedIsland(vector<vector<int>>& grid) {
int res = 0;
// 先将边缘的岛屿给淹了
for (int i = 0; i < grid.size(); i++) {
dfs(grid, i, 0);
dfs(grid, i, grid[0].size() - 1);
}
for (int j = 0; j < grid[0].size(); j++) {
dfs(grid, 0, j);
dfs(grid, grid.size() - 1, j);
}
// 再判断岛屿个数
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == 0) {
res++;
dfs(grid, i, j);
}
}
}
return res;
}
void dfs(vector<vector<int>> &grid, int i, int j) {
if ((i >= grid.size() || j >= grid[0].size() || i < 0 || j < 0)) {
return;
}
if (grid[i][j] == 1) {
return;
}
// 不断把四周淹了
grid[i][j] = 1;
dfs(grid, i-1, j);
dfs(grid, i+1, j);
dfs(grid, i, j-1);
dfs(grid, i, j+1);
}
};
最小覆盖子串 (经典滑动窗口)
class Solution {
public:
string minWindow(string s, string t) {
// 滑动窗口框架,左闭右开
int left = 0, right = 0;
unordered_map<char, int> need, window;
int valid_num = 0; // 滑动窗中满足答案的字符串个数
int start = 0; int len = INT_MAX; // 最终答案在字符串中的起始索引和长度
for (auto & i: t) need[i]++;
while (right < s.size()) {
char cur = s[right];
right++;
// 当前字符是我们需要的
if (need.count(cur)) {
window[cur]++;
// 有一个字符达到个数之后就使 valid_num++
if (window[cur] == need[cur]) {
valid_num++;
}
}
// 所有的字符都达到个数之后就开始收缩窗口
while (valid_num == need.size()) {
if (right - left < len) {
start = left;
len = right - left;
}
char left_cur = s[left];
left++;
if (need.count(left_cur)) {
if (window[left_cur] == need[left_cur]) {
valid_num--;
}
// window 缩减要放在后面,不然会对 valid 的结果产生影响
// 其实 left 和 right 做的事情是对称的
window[left_cur]--;
}
}
}
return len == INT_MAX ? string() : s.substr(start, len);
}
};
rand3() 实现 rand4()
有两种,一种是从 0 开始的 rand 函数,一种是从 1 开始的 rand,不管是哪样的,做法就是先生成等概率的均匀分布,再筛除一些不需要的元素,最后根据取余操作或者整除操作来获得我们想要的结果。从构造均匀分布来说的话,如果是从 0 开始的话就是 (randX())*(X+1) + randX(),如果是从 1 开始的话就是 (randX()-1)*X + randX()
import numpy as np
# 用 rand3: 1,2,3 生成 rand4
def rand3():
return np.random.randint(1, 4)
def rand4():
while 1:
#构造1~9的均匀分布
res = (rand3()-1) * 3 + rand3()
#剔除大于8的值,1-8等概率出现
if res <= 8:
break
return res % 4 + 1
# 用 rand3: 0,1,2,3 生成 rand4
def rand3():
return np.random.randint(0, 4)
def rand4():
while 1:
res = (rand3()) * 4 + rand3()
if res <= 14:
break
return res % 5
def main():
a = dict()
b = dict()
for i in range(50000):
r3 = rand3()
r4 = rand4()
if r3 in a.keys():
a[r3] += 1
else:
a[r3] = 1
if r4 in b.keys():
b[r4] += 1
else:
b[r4] = 1
print(sorted(a.items(), key=lambda e:e[0], reverse=False))
print(sorted(b.items(), key=lambda e:e[0], reverse=False))
if __name__ == '__main__':
main()
正则表达式 (TODO)
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size() + 1, n = p.size() + 1;
vector<vector<bool>> dp(m, vector<bool>(n, false));
dp[0][0] = true;
// 初始化首行
for(int j = 2; j < n; j += 2)
dp[0][j] = dp[0][j - 2] && p[j - 1] == '*';
// 状态转移
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if(p[j - 1] == '*') {
if(dp[i][j - 2]) dp[i][j] = true; // 1.
else if(dp[i - 1][j] && s[i - 1] == p[j - 2]) dp[i][j] = true; // 2.
else if(dp[i - 1][j] && p[j - 2] == '.') dp[i][j] = true; // 3.
} else {
if(dp[i - 1][j - 1] && s[i - 1] == p[j - 1]) dp[i][j] = true; // 1.
else if(dp[i - 1][j - 1] && p[j - 1] == '.') dp[i][j] = true; // 2.
}
}
}
return dp[m - 1][n - 1];
}
};
最长回文子串 (双指针中心开花)
class Solution {
public:
string longestPalindrome(string s) {
// 回文串可能是单数可能是双数
string res;
for (int i = 0; i < s.size(); i++) {
string s_single = hwstring(s, i, i);
string s_double = hwstring(s, i, i+1);
// 进行比较
res = res.size() > s_single.size() ? res : s_single;
res = res.size() > s_double.size() ? res : s_double;
}
return res;
}
string hwstring(string s, int l, int r) {
while (l >= 0 && r < s.size()) {
if (s[l] == s[r]) {
l--;
r++;
} else {
break;
}
}
// start, size
int size = (r-1)-(l+1)+1;
return s.substr(l+1, size);
}
};
下一个更大的元素/每日温度 (单调栈)
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> stk;
vector<int> res(temperatures.size());
// 倒着遍历,这样的话就是 pop 就是正序
for (int i = temperatures.size()-1; i >= 0; i--) {
// 把后面的矮过当前元素的值都给 pop 出来
while (!stk.empty() && temperatures[stk.top()] <= temperatures[i]) {
stk.pop();
}
// 空的时候说明是最后一个,或者后面的元素没有比他大的(之前已经把矮的给 pop 出来了)
res[i] = stk.empty() ? 0 : stk.top()-i;
stk.push(i);
}
return res;
}
};
数据流中的中位数 (大小顶堆)
class MedianFinder {
public:
// 输入的时候将数字分为两半,小的一半放在大根堆small中,大的一半放在小根堆的big中。
// 输入的同时保证两堆的大小之差不超过一,如果超过,则将数量多的堆弹出堆顶元素放到另一个堆中。
// 取中位数的时候,奇数返回数量多的堆顶元素;偶数返回两堆的堆顶平均数即可。
/** initialize your data structure here. */
priority_queue<int> smaller;
priority_queue<int, vector<int>, greater<int>> bigger;
int n = 0;
MedianFinder() {
}
void addNum(int num) {
// 分成两半,小的一半放在大根堆small中,大的一半放在小根堆的big中
// 相当于一个普通班一个实验班,将普通班的最屌的放入实验班,将实验班的最菜的放入普通班
if (smaller.empty()) {
smaller.push(num);
n++;
return; // 别忘了 return,否则就会执行到后面的句子
}
if (num < smaller.top()) {
smaller.push(num);
n++;
} else {
bigger.push(num);
n++;
}
// 这题很坑,不能直接 if (smaller.size() - bigger.size() > 1)
// 因为 .size() 返回的是 unsigned int,加减的时候可能转成补码变成了很大的数
int s_size = smaller.size(), b_size = bigger.size();
if (s_size - b_size > 1) {
bigger.push(smaller.top());
smaller.pop();
}
if (b_size - s_size > 1) {
smaller.push(bigger.top());
bigger.pop();
}
}
double findMedian() {
if (n % 2) {
return bigger.size() > smaller.size() ? bigger.top() : smaller.top();
} else {
return (smaller.top() + bigger.top()) / 2.0;
}
}
};
乘积最大的子数组
class Solution {
public:
int maxProduct(vector<int>& nums) {
int res = nums[0];
int min_val = res, max_val = res;
for (int i = 1; i < nums.size(); i++) {
// 如果数组的数是负数,那么会导致最大的变最小的,最小的变最大的。因此交换两个的值。
if (nums[i] < 0) {
swap(min_val, max_val);
}
max_val = max(max_val * nums[i], nums[i]);
min_val = min(min_val * nums[i], nums[i]);
res = max(max_val, res);
}
return res;
}
};
n 数之和
就是递归调用 n 数之和,base case 就是两数之和,先排序然后去重
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
// n 为 3,从 nums[0] 开始计算和为 0 的三元组
return nSumTarget(nums, 3, 0, 0);
}
/* 注意:调用这个函数之前一定要先给 nums 排序 */
// n 填写想求的是几数之和,start 从哪个索引开始计算(一般填 0),target 填想凑出的目标和
vector<vector<int>> nSumTarget(
vector<int>& nums, int n, int start, int target) {
int sz = nums.size();
vector<vector<int>> res;
// 至少是 2Sum,且数组大小不应该小于 n
if (n < 2 || sz < n) return res;
// 2Sum 是 base case
if (n == 2) {
// 双指针那一套操作
int lo = start, hi = sz - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) {lo++;}
} else if (sum > target) {
while (lo < hi && nums[hi] == right) {hi--;}
} else {
res.push_back({left, right});
while (lo < hi && nums[lo] == left) {lo++;}
while (lo < hi && nums[hi] == right) {hi--;}
}
}
} else {
// n > 2 时,递归计算 (n-1)Sum 的结果
for (int i = start; i < sz; i++) {
vector<vector<int>>
sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (vector<int>& arr : sub) {
// (n-1)Sum 加上 nums[i] 就是 nSum
arr.push_back(nums[i]);
res.push_back(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}
};
把数组排成最小的数
https://leetcode.cn/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof/
// 主要就是这个比较函数难想到!
class Solution {
public:
// 要加上 static,不然的话报错
static bool cmp(string a, string b) {
return a+b < b+a;
}
string minNumber(vector<int>& nums) {
vector<string> t;
for (auto &i: nums) {
t.emplace_back(to_string(i));
}
sort(t.begin(), t.end(), cmp);
// 或者用 lambda 函数
// sort(t.begin(), t.end(), [](string& x, string& y){ return x + y < y + x; });
string res;
for (int i = 0; i < t.size(); i++) {
res += t[i];
}
return res;
}
};
顺时针旋转矩阵90度
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
// 先沿着向右的斜对角线创建镜像矩阵,注意 j 从 i 开始,不是 0
// 逆时针转的话也是一样的,只不过是向左的斜对角线
int r = matrix.size(), c = matrix[0].size();
for (int i = 0; i < r; i++) {
for (int j = i; j < c; j++) {
swap(matrix[i][j], matrix[j][i]);
}
}
// 再将每一行都反转(双指针)
for (int i = 0; i < r; i++) {
int left = 0, right = c-1;
while (left < right) {
swap(matrix[i][left], matrix[i][right]);
left++;
right--;
}
}
}
};
顺时针打印矩阵
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
if (!matrix.size()) {
return res;
}
// 确定四个边界
int left_bound = 0;
int right_bound = matrix[0].size() -1;
int up_bound = 0;
int bottom_bound = matrix.size() -1;
// 开始往四个方向顺时针遍历
while (res.size() < matrix.size() * matrix[0].size()) {
// traverse left->right
if (up_bound <= bottom_bound) {
for (int i = left_bound; i <= right_bound; i++) {
res.emplace_back(matrix[up_bound][i]);
}
up_bound++;
}
// traverse up->bottom
if (left_bound <= right_bound) {
for (int i = up_bound; i <= bottom_bound; i++) {
res.emplace_back(matrix[i][right_bound]);
}
right_bound--;
}
// traverse right->left
if (up_bound <= bottom_bound) {
for (int i = right_bound; i >= left_bound; i--) {
res.emplace_back(matrix[bottom_bound][i]);
}
bottom_bound--;
}
// traverse bottom->up
if (left_bound <= right_bound) {
for (int i = bottom_bound; i >= up_bound; i--) {
res.emplace_back(matrix[i][left_bound]);
}
left_bound++;
}
}
return res;
}
};
x 的平方根 (牛顿迭代法)
给你一个非负整数
x,计算并返回x的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
class Solution {
public:
// 首先随便猜一个近似值 xx,然后不断令 xx 等于 xx 和 a/xa/x 的平均数,
// 迭代个六七次后 xx 的值就已经相当精确了。
int mySqrt(int x) {
if (!x) {
return x;
}
long long res = x;
while (res*res > x) {
res = (res + x/res) / 2;
}
return res;
}
};