preface
numpy 早就用过了,但是长时间不用的话对其中的一些知识点又会忘记,又要去网上翻看各种博客,干脆自己把常用的一些东西记下来好了,以后忘了的话直接看自己写的笔记就行了
numpy 基础
numpy 是 python 的矩阵运算库,底层由 C++ 编写,因此速度相比 python 自身快得多,经常用于数据科学领域中,语法和 Matlab 有些相似。
numpy(下面简称 np)的基本类型是 ndarray(n dimensions array),又用 np.array 称呼它,它有很多属性:np.ndim 表示数组的维度,np.size 表示数组中元素的个数,np.shape 表示数组各个维度的大小,例如一个三行四列矩阵的 shape 就是(3, 4),np.dtype 表示数组的数据类型,np 里面有很多的数据类型,如 np.int32,np.int16,np.float64,np.complex 等等

创建 array
可以用特定的数据来创建一个 array 矩阵,只需要在 np.array() 的括号中传入一个列表作为参数就行了,多维的 array 传入多重列表就行,并且还可以顺便加上 dtype 参数指定 array 的数据类型

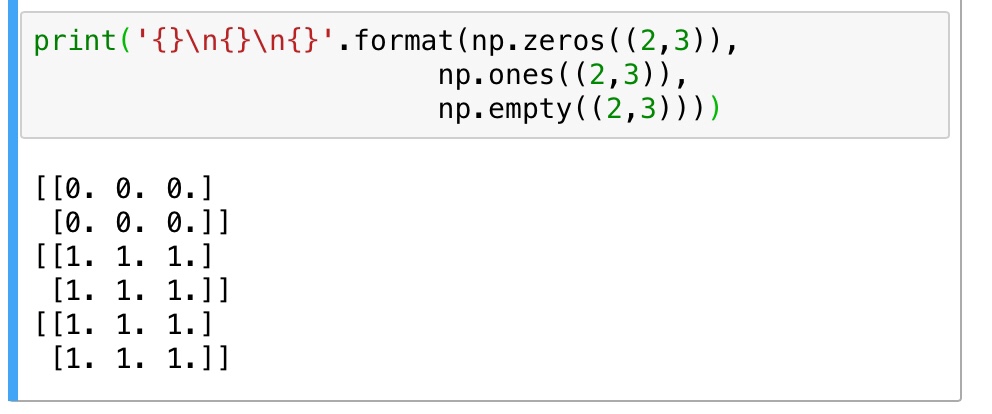
不过这样子创造 array 太累了,如果我只是想捏造一些数据来做实验而已的话完全可以用 np 内置的函数来快速生成一个 array。np.zeros((size), dtype) 生成零矩阵,np.ones((size), dtype) 生成单位阵,np.empty((size), dtype) 生成的矩阵的值是随机初始化的,和内存的状态有关,默认情况下,如果不显示指明 dtype,用这些函数生成的 array 都是 np.float64 类型的
还有一种方法是用 np.arange(begin, end, step) 通过一个数字序列来生成 array ,很像 python 中创建列表的 range 方法,同样也是 “包头不包尾” ,还有np.linspace(begin, end, count) 用来创建从 begin 到 end-1 范围内,拥有 count 个元素的 array。

当然也还有创建随机矩阵,这个是挺常用的,一般用 np.random.random() 来创建,里面接受一个 tuple 型的参数,代表 array 各个维度的大小,还有一种 np.random.randn() 也是常用的,里面接受任意个参数来代表各个维度的大小,如果是三维的 array 就传入三个参数,用 randn 方法生成的数据是基于标准差为 1 ,u = 0 的正态分布数据。

基本运算
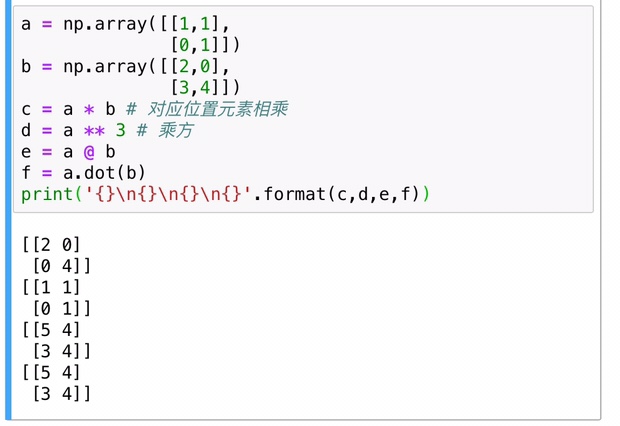
四则运算中,加法和减法在 np 中还是通用的,因为 np 主要操作对象是矩阵,所以乘法除法另说,* 在 np 中指的是对每一个元素进行的乘法(elementwise),矩阵相乘在 np 中用 @ 或者 np.dot 来操作,没有除法,只有用 np.linalg.inv 对矩阵进行求逆矩阵操作
除此之外,np 也可以对 array 的每一列每一行都进行操作,比如求每一行或每一列的最大最小值,ndarray 对象提供了 sum,min,max(axis=0/1) 等统计方法,axis = 0 时对象为每一列,axis = 1 的对象为每一行

以及还有很多通用函数,如 np.sqrt,np.sin,np.exp 等等等等说不完,只要看到函数名字应该就能够知道他们是干什么的了,使用时看看手册便 OK
slice & index & iteration
np 的切片和索引和 python 是差不多的,甚至有些地方比 python 的还要更加高级一些,np 的多维矩阵的每个维度都可以运用切片,不同维度之间用逗号隔开,... 代表其他维度都按默认全部切片
x[1,2,…] is equivalent to x[1,2,:,:,:], x[…,3] to x[:,:,:,:,3] and x[4,…,5,:] to x[4,:,:,5,:]

迭代默认是按照第一个维度进行迭代,也就是一行一行输出,如果要想将 array 中的元素全部输出用 for element in array.flat 进行迭代。
np 的高级索引,不像 python 只能用字符和数字做索引,np 还可以用整形矩阵和布尔型矩阵来进行索引,虽然平时可能用的并不多。还可以用多维矩阵做索引,有点类似函数的感觉,看个例子就知道了

改变 shape
前面就已经给出了几个改变 array 的 shape 的方法了,在 np 中有 ndarray.reshape,ndarray.T,ndarray.resize,ndarray.ravel 等几个常用的进行变形的方法,其中 reshape 和 resize 的效果是一样的,不过 reshape 会返回一个新的 array ,而 resize 是在原来的 array 上就地修改,并且,为了方便,reshape 可以在确定了其中一个维度的大小后将另一个维度用 -1 表示,让计算机自己去计算,但是用 resize 的话一定要将所有的维度都正确填写,不能偷懒。ravel 是将 array 平摊成一行展开变成一个一行的矩阵

堆叠和拆分
这部分用得比较少吧?但是还是记一下,堆叠也就是将两个矩阵变成一个矩阵,有点类似增广矩阵的意思,拆分就是把一个矩阵拆成好多个小矩阵,np 中用 stack 和 split 关键字来处理。
堆叠有水平堆叠 np.hstack 和垂直堆叠 np.vstack,两个函数都接受一个 tuple 参数,tuple 中是要进行合并的两个矩阵,既然要合并的话,两个矩阵在合并方向上的维度大小一定要一致才行:例如用 vstack 进行垂直合并的话,就得保证合并的两个矩阵的列数要一致

拆分道理差不多,用的比较少就不说了,需要用的时候再去看手册好啦
深浅拷贝
这个概念在很多编程语言里面都有,一旦理解的话可以运用到其他的地方,底层来说的话,浅拷贝相当于拷贝前后的两个变量公用一块内存,改变了其中一个的话,另一个也会跟着改变,深拷贝则是开辟了另一块内存进行拷贝,使拷贝前后二者没有任何关联,仅仅是值相等,改变其中一个的值另一个并不会跟着改变。
np 中有点不同,如果直接将矩阵赋值给另一个矩阵,相当于没有拷贝,只是给矩阵换了个名字而已,因此如果有 a = b,b 改变的同时 a 也会改变。

np 的浅拷贝用 np.view() 来实现,view 只分享数据给另一个矩阵,b = a.view(),此时 b 就是 a 浅拷贝后的矩阵,a 改变 shape 后 b 的 shape 不改变,但是 a 改变数据的值后 b 的值也会改变。(值得注意的是 np 的切片返回的是原矩阵的浅拷贝,见下图中的例子)


深拷贝用 np.copy() 实现,深拷贝并不会和原矩阵共享任何东西,原矩阵有任何变化都不会影响深拷贝得到的矩阵

线性代数
np 是为矩阵操作而设计的,所以里面也有很多的线性代数方面的接口,比如求逆 np.linalg.inv,求转置 np.transpose,创建单位阵 np.eye ,求矩阵的迹 np.trace,其实跟 matlab 里面的函数是差不多的,所以还是比较好掌握的,主要是理解线性代数中矩阵各种性质的原理。
广播
广播机制很好用,很牛逼,但是能被广播是需要条件的:
- 两个数组各维度大小从后往前均一致(不够的维度就不用管)
- 两个数组存在一些维度大小不相等时,有一个数组的该不相等维度大小为 1 (所以有些代码会用到很多增加一个维度的操作,就是为了能用广播)
A = np.zeros((2,5,3,4))
B = np.zeros((3,4))
print((A+B).shape)
print((A*B).shape)
A = np.zeros((4))
B = np.zeros((3,4))
print((A+B).shape)
print((A*B).shape)
A = np.zeros((2,5,3,4))
B = np.zeros((3,1))
print((A+B).shape)
print((A*B).shape)
A = np.zeros((2,5,3,4))
B = np.zeros((2,1,1,4))
print((A+B).shape)
print((A*B).shape)
A = np.zeros((1))
B = np.zeros((3,4))
print((A+B).shape)
print((A*B).shape)
输出结果
(2, 5, 3, 4)
(2, 5, 3, 4)
(3, 4)
(3, 4)
(2, 5, 3, 4)
(2, 5, 3, 4)
(2, 5, 3, 4)
(2, 5, 3, 4)
(3, 4)
(3, 4)
numpy with pytorch
np.newaxis
这个 api 相当于 None,就是说 np.newaxis == None 返回值是 True,那么这个玩意有什么作用呢,它是用来增加数据的维度的,在 pytorch 里面经常用到,把 np.newaxis 换成 None 也是一样的(默认增加的是第零维的维度)
# 一维情况
a = np.array([1,2,3,4,5])
a
array([1, 2, 3, 4, 5])
b = a[np.newaxis]
b
array([[1, 2, 3, 4, 5]])
# 多维情况
aa = np.array([[1,2,3,4],[4,5,6,7]])
aa
array([[1, 2, 3, 4],
[4, 5, 6, 7]])
bb = aa[np.newaxis]
bb
array([[[1, 2, 3, 4],
[4, 5, 6, 7]]])
aa.shape
(2, 4)
bb.shape
(1, 2, 4)
bb = aa[:,np.newaxis]
bb
array([[[1, 2, 3, 4]],
[[4, 5, 6, 7]]])
aa
array([[1, 2, 3, 4],
[4, 5, 6, 7]])
bb.shape
(2, 1, 4)
bb = aa[:,:,np.newaxis]
bb
array([[[1],
[2],
[3],
[4]],
[[4],
[5],
[6],
[7]]])
reference: https://www.itread01.com/content/1547568207.html
np.meshgrid
simple-faster-rcnn 中有用到这个,记录一下。[X, Y] = meshgrid(x,y) 将向量 x 和 y 定义的区域转换成矩阵 X 和 Y , 其中矩阵 X 的行向量是向量 x 的简单复制,而矩阵 Y 的列向量是向量 y 的简单复制 (注:下面代码中 X 和 Y 均是数组,在文中统一称为矩阵了)。
假设 x 是长度为 m 的向量,y 是长度为 n 的向量,则最终生成的矩阵 X 和 Y 的维度都是 n * m(注意不是 m * n)
import numpy as np
x = np.arange(0, 5)
print(x)
print('-------------')
y = np.arange(1, 3)
print(y)
print('-------------')
X, Y = np.meshgrid(x, y)
print(X)
print('-------------')
print(Y)
print('-------------')
[0 1 2 3 4]
-------------
[1 2]
-------------
[[0 1 2 3 4]
[0 1 2 3 4]]
-------------
[[1 1 1 1 1]
[2 2 2 2 2]]
-------------
reference: https://www.cnblogs.com/lemonbit/p/7593898.html
np.argsort
argsort 函数返回的是数组值从小到大的索引值,也就是 index
一维数组
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0])
>>> x.argsort()
array([1, 2, 0])
二维数组
>>> x = np.array([[0, 3], [2, 2]])
>>> np.argsort(x, axis=0) #按列排序
array([[0, 1],
[1, 0]])
>>> np.argsort(x, axis=1) #按行排序
array([[0, 1],
[0, 1]])
降序排列
>>> x = np.array([3, 1, 2])
>>> np.argsort(-x)
array([0, 2, 1])
或者另一种方式
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)[::-1]
array([0, 2, 1])
np.append
其实很 python 列表的 append 是挺像的
annotations = np.zeros((0, 5))
annotation = np.zeros((1, 5))
annotation[0, :] = 1,2,3,4,5
annotations = np.append(annotations, annotation, axis=0)
annotations = np.append(annotations, annotation, axis=0)
annotations
array([[1., 2., 3., 4., 5.], [1., 2., 3., 4., 5.]])
np.expand_dims
用来增加 array 的维度,通过传入 axis 参数来控制在哪个维度上添加
import numpy as np
a = np.array([1, 2, 3])
print(a.shape)
# a.shape(3,)
b = np.expand_dims(a, axis=0)
b = [[1, 2, 3]]
# b.shape = (1, 3)
np.tile
numpy.tile(A, reps) 用来将 A 的元素重复 reps 次,类似与 numpy 的广播机制,不过文档强烈建议直接用广播机制不要用这个函数
>>> c = np.array([1,2,3,4])
>>> np.tile(c, 4)
array([1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4])
>>> np.tile(c, (4,1))
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
np.dot 和 np.matmul
当两个矩阵是向量时,可以用 dot 来计算两者的点积,是一个数,当两个矩阵是二维矩阵时,用 dot 得到的是一个矩阵。用 matmul 是一样的,也是计算两个矩阵相乘的结果
>>> import numpy as np
>>> a = np.array([[1,2,3],[4,5,6]])
>>> b = np.array([[1,2],[3,4],[5,6]])
>>> np.matmul(a,b)
array([[22, 28],
[49, 64]])
>>> np.dot(a,b)
array([[22, 28],
[49, 64]])
np.linalg.norm
norm 表示范数,这个 api 用来求范数 np.linalg.norm(x, ord=None, axis=None, keepdims=False)。默认情况下求的是二范数,也就是对应位置元素相乘再相加再开方
axis:处理类型
axis=1表示按行向量处理,求多个行向量的范数
axis=0表示按列向量处理,求多个列向量的范数
axis=None表示矩阵范数
keepding:是否保持矩阵的二维特性
True表示保持矩阵的二维特性,False相反
import numpy as np
x = np.array([
[0, 3, 4],
[1, 6, 4]])
#默认参数ord=None,axis=None,keepdims=False
print("默认参数(矩阵整体元素平方和开根号,不保留矩阵二维特性):",np.linalg.norm(x))
print("矩阵整体元素平方和开根号,保留矩阵二维特性:",np.linalg.norm(x,keepdims=True))
print("矩阵每个行向量求向量的2范数:",np.linalg.norm(x,axis=1,keepdims=True))
print("矩阵每个列向量求向量的2范数:",np.linalg.norm(x,axis=0,keepdims=True))
print("矩阵1范数:",np.linalg.norm(x,ord=1,keepdims=True))
print("矩阵2范数:",np.linalg.norm(x,ord=2,keepdims=True))
print("矩阵∞范数:",np.linalg.norm(x,ord=np.inf,keepdims=True))
print("矩阵每个行向量求向量的1范数:",np.linalg.norm(x,ord=1,axis=1,keepdims=True))
默认参数(矩阵整体元素平方和开根号,不保留矩阵二维特性): 8.831760866327848 矩阵整体元素平方和开根号,保留矩阵二维特性: [[8.83176087]] 矩阵每个行向量求向量的2范数: [[5. ] [7.28010989]] 矩阵每个列向量求向量的2范数: [[1. 6.70820393 5.65685425]] 矩阵1范数: [[9.]] 矩阵2范数: [[8.70457079]] 矩阵∞范数: [[11.]] 矩阵每个行向量求向量的1范数: [[ 7.] [11.]]
np.transpose
和 torch.premute 一样,都是对维度进行置换,只不过这个针对的是 numpy,permute 针对的是 tensor,在进行可视化的时候经常会用到这个函数,一般用法如下
vis_img = np.transpose(a, (1,2,0))