preface
之前介绍了那么多的理论知识,现在开始终于要着手训练神经网络了,这里就记录一下相关的知识点
训练流程
训练一个神经网络通常有以下几个流程:1. 训练前设置好相关的参数,如激活函数,预处理,权重初始化,正则化,检查梯度;2. 开始训练模型,再训练的过程中观察学习的过程,以及参数的更新和超参数优化问题;3. 评估模型,测试模型的准确率和帧率。下面我们就一个一个步骤来说说
Activation Functions
在之前的文章中我们就已经初步了解了激活函数的作用了,也就是一个非线性的函数,如果没有激活函数的话,神经网络层数再高也只是个线性的矩阵相乘而已,用了激活函数就使得神经网络的非线性成分增多,能让网络学习更加复杂的东西,这里详细价绍几个激活函数的特性以及方程
sigmoid
sigmoid 函数的方程表达式这样的: $\sigma(x) = 1 / (1 + e^{-x})$ ,下面是它的函数图像
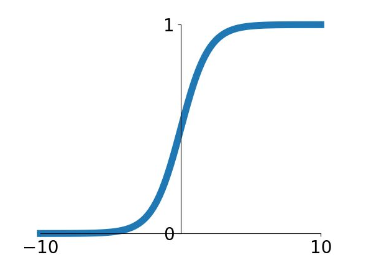
从图像上可以看出 sigmoid 函数的输出值在 (0, 1)区间里面,输出范围是有限的,因此优化稳定可以用作输出层,并且这是个连续函数,方便我们的求导。但是 sigmoid 的缺点也是挺多的
- sigmoid 函数在输入非常大或非常小的时候会出现饱和现象,也就是说函数对输入的改变变得很不敏感,此时函数特别平,导数为 0,意味着反向传播时梯度接近于 0,这样权重基本不会更新,会造成梯度消失的情况从而无法完成深层网络的训练
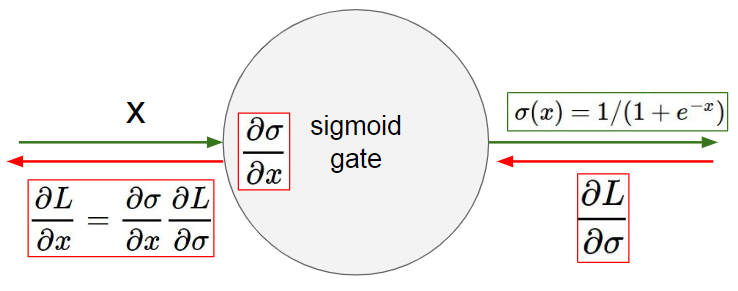
- sigmoid 的输出不是零均值的,这是由它的函数性质决定的,这样的话反向传播时,$\frac{\partial L}{\partial w} = \frac{\partial L}{\partial \sigma}\frac{\partial \sigma}{\partial w}$ ,W 的梯度要么全是正的要么全是负的,这就可能会造成梯度按照 zig-zag 蛇形下降,不过这也只是在单个元素的情况下才会发生,用 minibatch 可以减少这种情况
- sigmoid 函数里面用到了指数函数,在计算上会有复杂度,不过这个跟神经网络训练参数相比还是九牛一毛,只是说在函数计算上会比较消耗算力
因此一般在神经网络的激活函数选择上,不会选用 sigmoid 这个函数,但用于二元分类问题的话还是可以作为输出层的函数使用
tanh
tanh 函数的公式是 $\tanh = \frac{\sinh x}{conh x} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$ ,图像如下
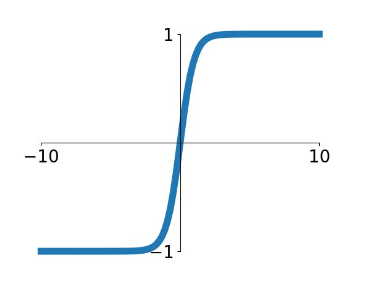
这跟 sigmoid 比起来有以下几点不同之处,首先 tanh 的输出是零均值的(看是不是零均值就看函数的图像是不是涵盖了 y 轴上下象限),这点很好,并且他将函数的输出值压缩到(-1,1)之间,但是他还是跟 sigmoid 一样存在梯度饱和以及指数运算的缺点
ReLU
ReLU(Rectified Linear Unit) 是非线性修正单元的缩写,公式是 $relu = max(0, x)$,图像如下
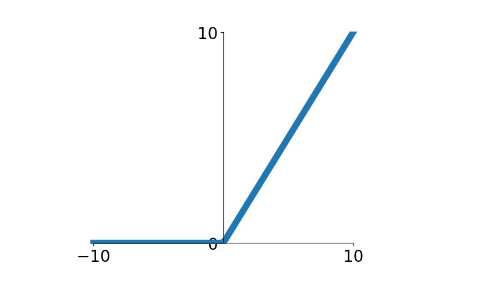
ReLU 不会出现梯度饱和以及梯度消失的问题,但是他的输出也不是零均值的,同时 ReLU 可能产生 Dead ReLU 情况,也就是在 x < 0 的时候,梯度变成 0,导致这个神经元以及之后的神经元梯度一直为 0 ,不再对任何数据有反应,导致相应的参数永远不会被更新,解决这种情况就得在初始化的时候将学习率降低
Leaky ReLU
Leaky ReLU 就在 ReLU 的基础上更新了一下,公式为 $Leaky relu = max(0.01, x)$ ,图像如下
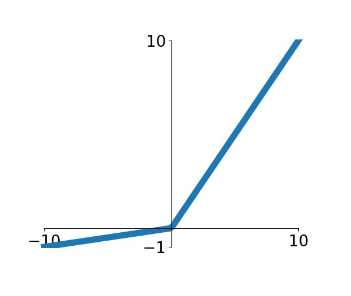
Leaky ReLU 解决了 Dead ReLU 的现象,用一个非常小的值来初始化神经元,使得 ReLU 在负数区更偏向于激活而不是 Dead
Maxout
关于 Maxout 可以看这篇文章,Maxout 并没有一个具体的函数表达式,他的思路就是用一个隐层来作为激活函数,隐层的神经元的个数可以由人为指定,是个超参数,但是缺点也很明显,加大了参数量以及计算量,并且还需要反向传播更新自身的权重系数
Data Processing
在处理数据之前,通常都要对数据进行预处理,我在模式识别课程上学过的有 PCA ,他是为了减少维度之间的冗余。先说个好消息,在卷积神经网络当中,通常不需要对数据进行太多的预处理,因为像素之间的差别很小。一般拿到数据后,首先要将数据进行零均值操作,以防止神经网络的输入量全是正的,在前面的文章里讲过了,如果输入量全是正的,那么反向传播时 W 的都是正的或者负的,会导致梯度按照 zig-zag 下降。
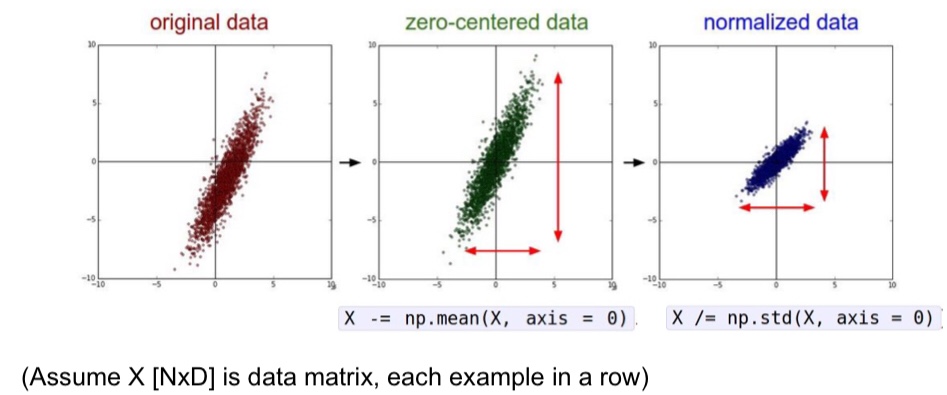
另外一个预处理操作就是 normalization 归一化了,归一化可以降低维度之间的差异性,防止某个特征的值太大,并且将特征归一到某个区间内能够加快梯度下降的速度,因为这样的话数据对于权重矩阵 W 的微小变化就不那么敏感了。
Weight Initialization
下面就到了权重初始化了,这也是有学问的, 神经元的 W 一开始应该赋予什么值呢?会对梯度下降产生怎样的影响?首先能够确定的是,肯定不能将 W 初始化为 0,初始化为 0 之后,每个神经元的输出都是一样的,根本学习不到东西,网上有人做了实验,用 0 去初始化 W ,可以看到在迭代 1000 次之后,loss 再也没有降下来,保持在 0.64 左右
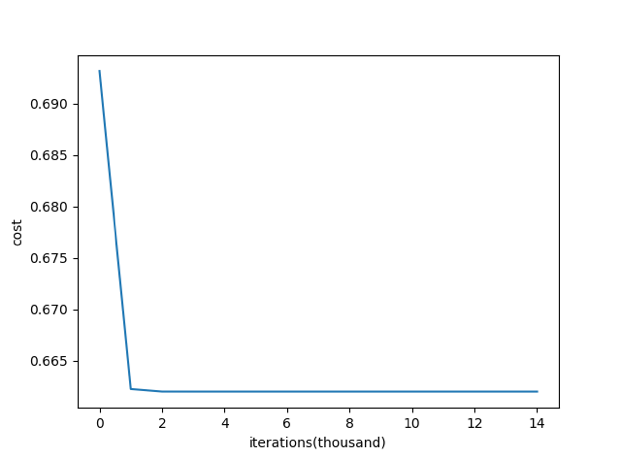
更通常的做法是用随机值初始化 W ,并且还要乘上一个很小的数例如 0.01,这是为了不让 W 过大,如果 W 太大并输入的 x 也很大的话,就容易使得激活函数的输入量过大,如果激活函数是 sigmoid 的话,就使得输出变成 0 或者 1 ,导致一些问题的发生(比如计算 loss function 时如果 function 中有 log 项的话就会使 log 里面变成 0 )。
python 里面一般用 numpy 的 random.randn() 来产生随机的矩阵,通过资料查询到 np.random.randn() 产生的是均值为 0,方差为 1 的随机数,因此这种方法对于层数不多的神经网络来说作用还是挺好的,但是对于深层的神经网络来说就不行了
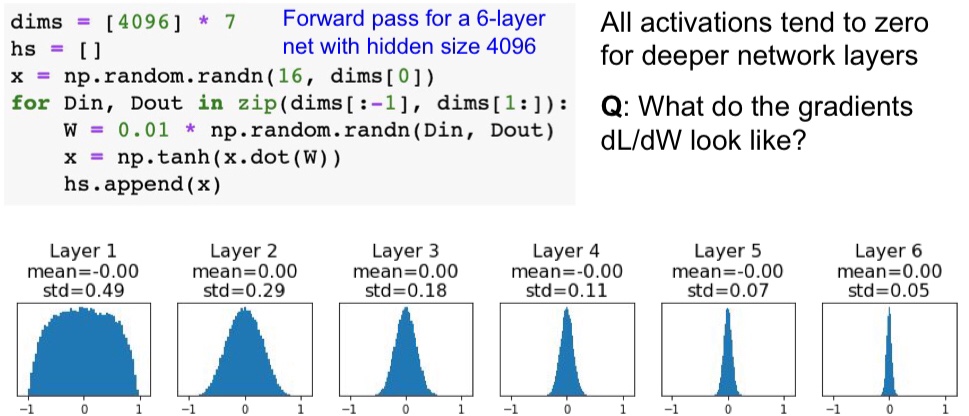
看看上图中输出的分布,激活函数是 tanh 函数。前面两层的分布在 -1 和 1 之间都挺均匀,层数越往后面,输出为 0 的分布就越大了,这会导致神经元反向传播时梯度为 0 ,这样子就学习不到东西。
那么将 W 初始化变得大一些呢,将 0.01 变成 0.05 试试,经过 tanh 函数,这下可以看到,第一层的输出直接就饱和了,全部集中在 -1 和 1 两边,这下应该直观地明白了为什么初始化的 W 不能太大的原因(狗头),这种饱和的情况会怎样呢,同样反向传播求偏导时,tanh 的导数为 0,由于链式法则导致梯度也为 0,还是学不到东西。

所以就有一种叫做 Xavier Initialization 的初始化方法出现了, 他的目的就是使得神经网络每一层的输出方差尽量相等,下面是用了 Xavier 初始化后的各层输出,可以看到深层的神经元的输出也符合漂亮的正态分布,这样就不会出现梯度为 0 的情况了,可以有效的使得输入量在经过多层神经网络之后的大小保持在一个合理的范围内,既不会太大也不会太小,减少了梯度的弥散,使信号能够传播到更深层的神经网络中。

但是使用 Xavier Initialization 是有条件的,那就是激活函数应该是线性的或者是接近线性的,并且也要求激活函数是零均值的,上面的 tanh 可以使用,但是 Relu 的话就不行了,网络的输出集中在 0 这个位置,反向传播时梯度又会消失,学不到东西。

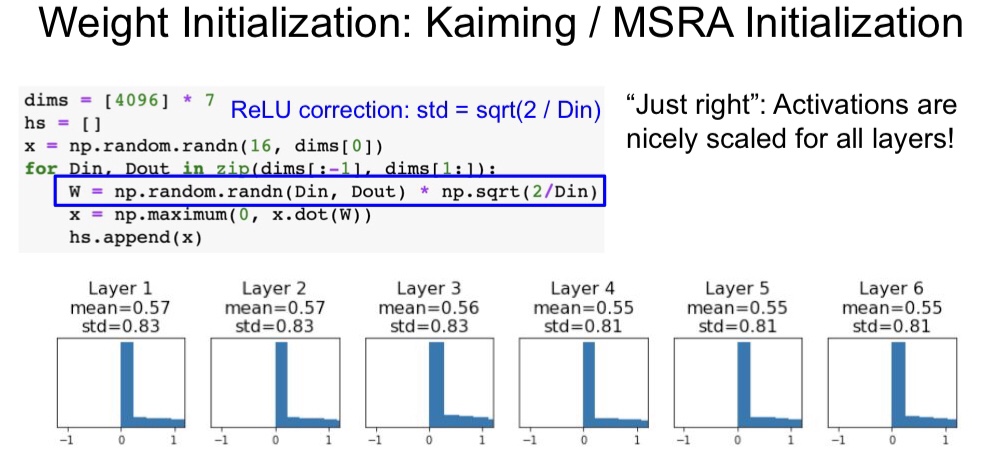
但是 Relu 不是用得最多的激活函数吗,不能用 Xavier 初始化那怎嘛办呢,也不要担心,我们的男神何恺明带来了自己的 He Initialization ,使得用了 Relu 系列的激活函数的神经元也能够很好的初始化权重 W ,如下图,每一层的输出的分布都很好,不会集中在 0 和 1 这两个端点。现在的神经网络在隐藏层常使用 Relu ,且权重初始化用 He Initialization
Batch Normalization
这一步是进行批归一化,至于它的作用呢,以后再说。。先鸽着
reference
https://zhuanlan.zhihu.com/p/92412922
https://blog.csdn.net/u012328159/article/details/80025785
https://blog.csdn.net/weixin_41770169/article/details/81561159
https://www.youtube.com/watch?v=wEoyxE0GP2M&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=6