preface
这节课就进入了正题讲起了卷积神经网络(Convolutional Neural Network),这应该是目前最流行的神经网络了,很多目标追踪算法和现代的应用都用到了卷积神经网络,学好这个才能算是入了深度学习的门,以前学过相关理论,因此这篇就写得简单点,主要是记录一下相应的知识点,加强一些概念性东西的理解。
卷积神经网络的结构
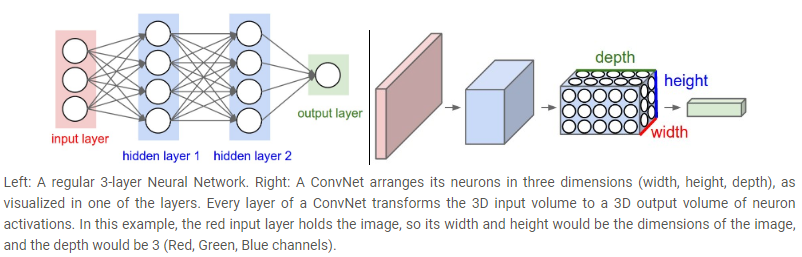
一般的神经网络的结构都差不多,都是由输入层,隐藏层,输出层组成的,卷积神经网络也一样,但它明确了输入层一定是一张图片,这就可以让我们大大减少网络中的参数量。注意,我们一般说神经网络的层数时是不会将输入层算进去的,因此下面左图就是一个三层的神经网络,右边的图就是它的模型图,卷积神经网络的输入是一张图片,因此会有长宽和深度(通道数),用来卷积的模板一般也是一个 3D 模型,卷积神经网络的输出一般是一个 N 维向量, N 代表着样本的类别数(类似分类器)
卷积层(conv layer)
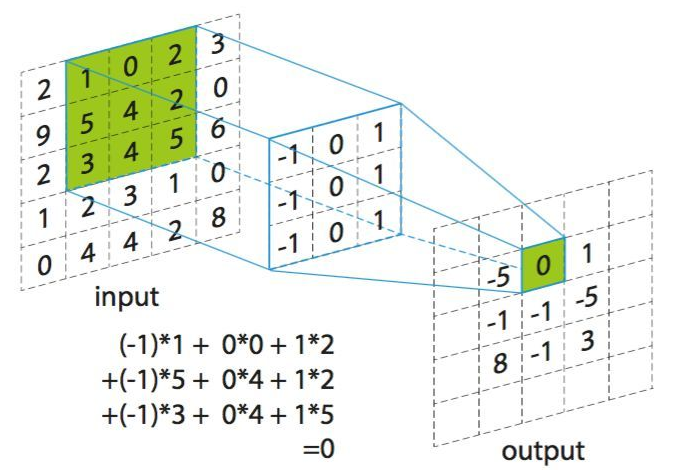
卷积神经网络最重要的特点就是进行图像之间的卷积了,这跟信号与系统里面说的对卷积是一样的意思,但在图像里面,卷积的数学意义就是对应位置的元素相乘然后再将所有结果相加。大体就是拿一个卷积模板在图像上滑动求卷积,最后会得到一个输出的图片,输出图片的大小与很多参数有关, 下面就来介绍一下相关参数
卷积的概念里面一般都有说要将信号翻转再卷积,这里没说是因为一般卷积模板都是对称的,翻转之后和之前是一样的
size F
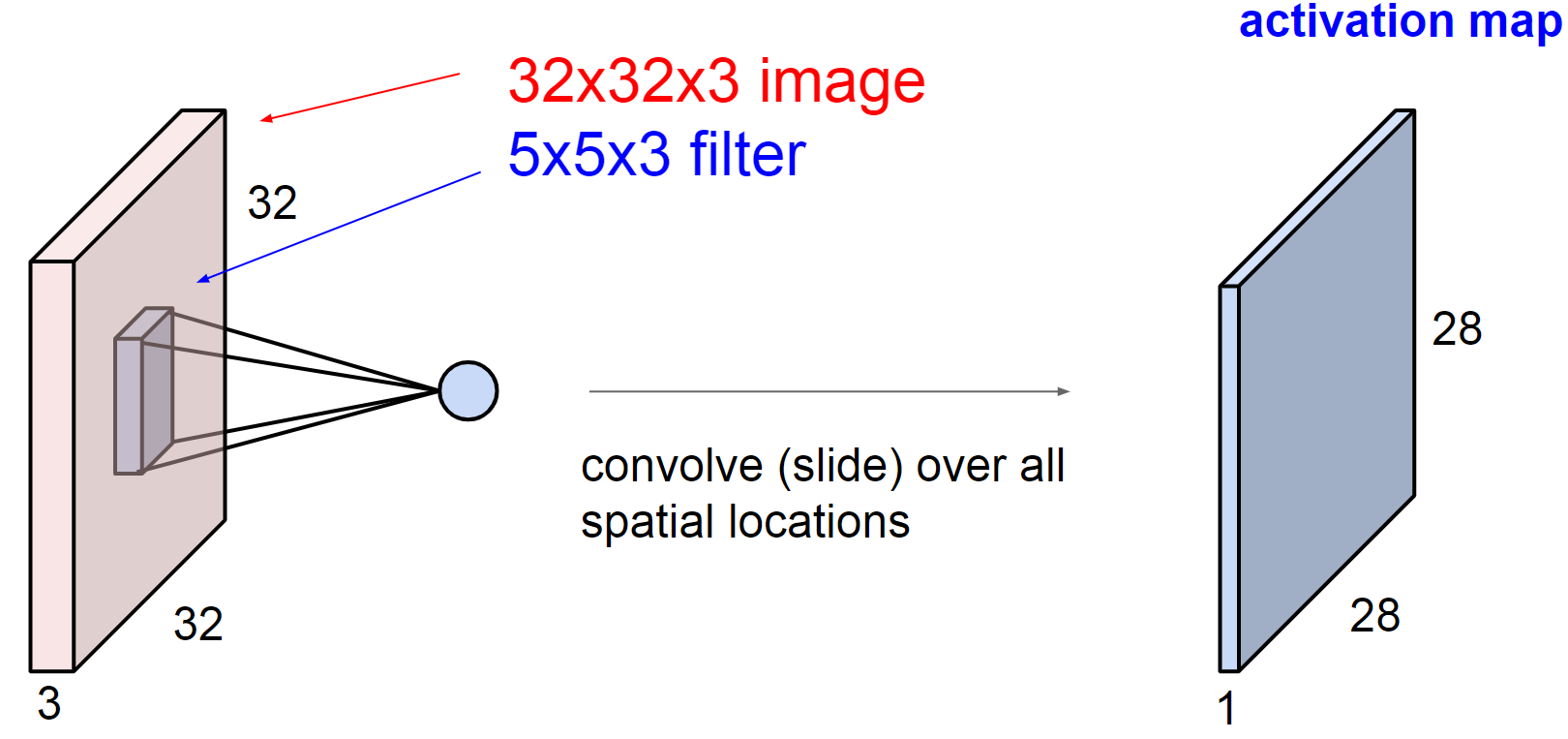
如下图,输入的是一张 32 x 32 x 3 的三通道图片,因此我们的卷积模板也得是 3 通道的,不然无法进行卷积操作。看最终的输出为 28 x 28 的单通道图,这是因为每一次卷积都是对三个通道上的所有元素进行相乘相加操作,因此最终只有一个通道,卷积模板是 5 x 5 的,因此输出图像大小为 32 - 5 + 1 = 28
如果我们的卷积模板是 1 x 1 的,不要认为这是没有意义的,始终记住我们处理的是深度图,因此用 1 x 1 的模板可以进行三维上的点积运算,使多个通道变成一个通道
number k
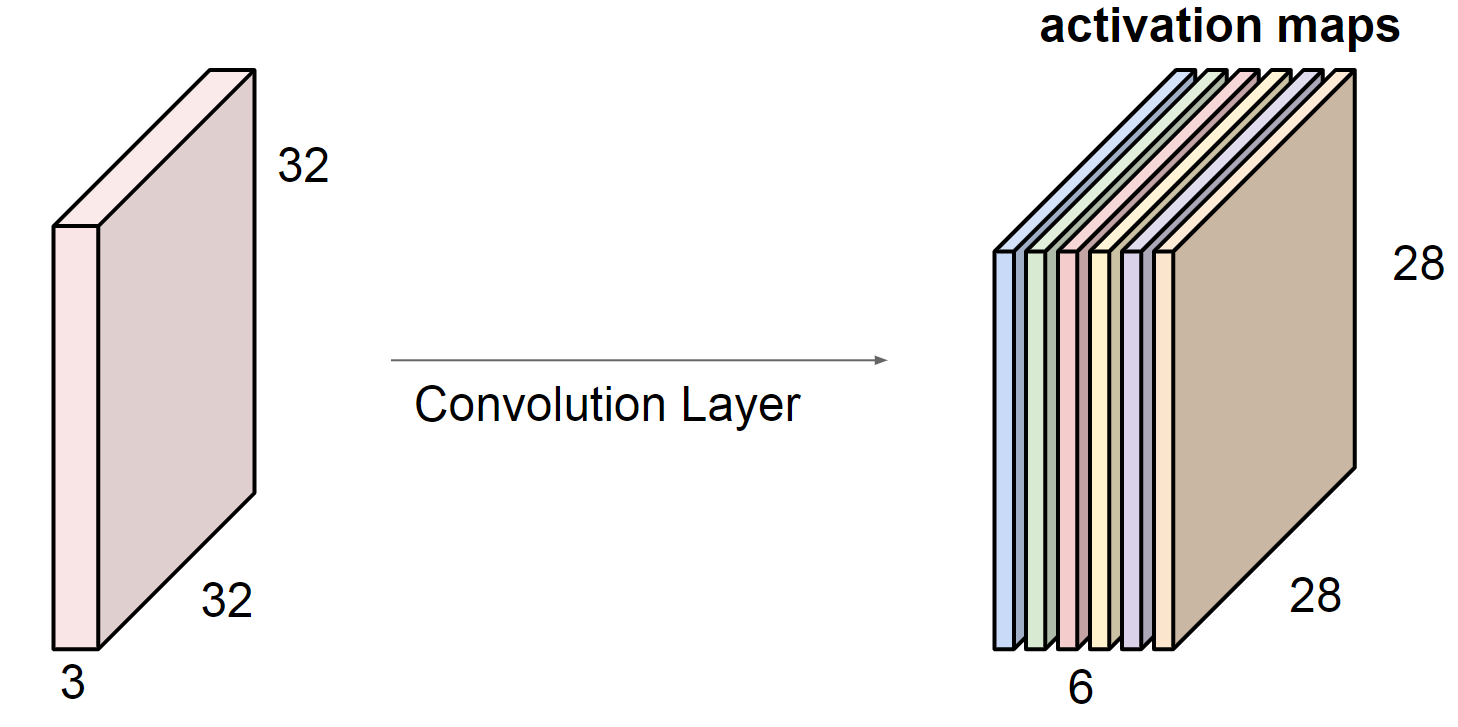
那么,如果我们在一个卷积层放入不止一个卷积核的话会怎么样呢,将相当于让很多单通道的输出图叠加在一起,就形成了一个多通道的输出了,下图就是在我们有 6 个 5 x 5 的卷积模板时的输出,形成了一个 6 通道的图,因此卷积模板的个数决定了输出的通道数,而且 k 一般是 2 的平方数,比如 32 64 128 等等
stride
我们上面的卷积都是逐个元素逐个元素滑动过去的,这样子的话每次的步长就是 1 ,也有步长不是 1 的,如果步长为 2 的话就说明卷积模板隔一个元素在卷积一次,这样的话最终的输出大小是怎样的呢,下面给出了对应的公式,一般步长为 2 的情况在池化层中经常碰到
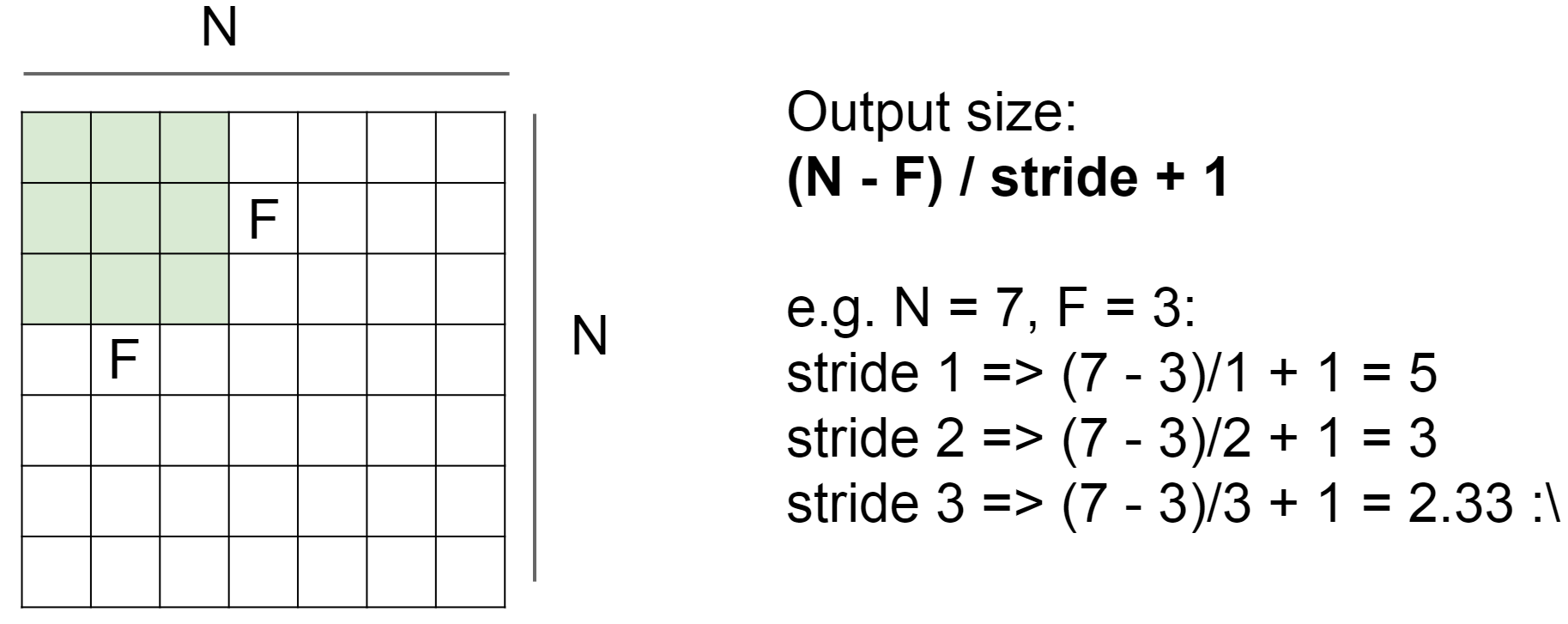
zero-padding
注意到,上面的卷积操作之后,输出的大小都会改变,如果想要输出的大小和输入的大小一样可以怎么办呢,一般的做法就是给输入层补零边,然后再卷积,该补多少边也是有讲究的,如果卷积核是 3 x 3 的,就补一圈, 5 x 5 的就补两圈,下面给出公式:

补零边除了在卷积之后可以保持输入的尺寸之外,还可以防止边缘信息被 ”迅速冲走“ :如果卷积层不对输入进行零填充,而仅执行有效的卷积,则在每次卷积之后,卷的大小将减少少量,并且边界上的信息将被“迅速冲走”
特征数
我们已经知道了每一层的输出就相当于是一个图片,在之前的学习中,我们也说了,一个权重矩阵说白了就是各个类的模板图像构成的矩阵,因此我们这里的输出也就是每一层的 W 权重矩阵,那么每一层的特征数是多少呢,也就是 W 中元素的个数再加上一个偏置 b (不要忘了加上 b)

神经元的角度
卷积的操作其实就跟神经网络的计算是一回事,只不过这个特征是以图片的形式呈现的,神经网络将特征全部都展开成一个向量来,并没有什么不同,都是先算 WTx + b ,再通过激活函数确定最终的输出

卷积的意义
卷积神经网络的思想就是卷积核的局部感受野(local field) 权值共享和下采样。卷积层使用的是卷积核,采用局部连接的方式,没有采用全连接,这样可以大大减少参数量,假设输入是 1000 * 1000 的图像,中间有 10 个神经元,如果是全连接的话就需要训练 10000000 个参数,如果每一个神经元只与局部 10 *10 个输入相连,则只需要 1000 个参数,再进一步,假设每个神经元都使用相同的权重(这就是权值共享),则所需训练的参数仅仅只有 100 个了。卷积核就是通过滑动窗的方式进行权值共享,每滑过一个区域,卷积核的参数都是一样的,不需要重新训练。
卷积核的用途是提取图像的特征,虽然一个卷积核能看见的区域有限(感受野),但是对于图像而言,局部区域的像素关联性往往很强,而相距较远的区域关联性往往很弱。因此,只需要对局部信息进行特征提取,最后综合起来就能达到全局感知。
池化层(pooling layer)
池化层的作用就是下采样,减少输出的特征数并且使得他们更方便管理,这个上过信号课程的同学都应该清楚,池化层一般用步长为 2 ,size 为 2 的模板,对模板中的元素进行处理,最终将模板中的 4 个元素变成一个输出,因此,这样输出的图片大小是之前的一半。
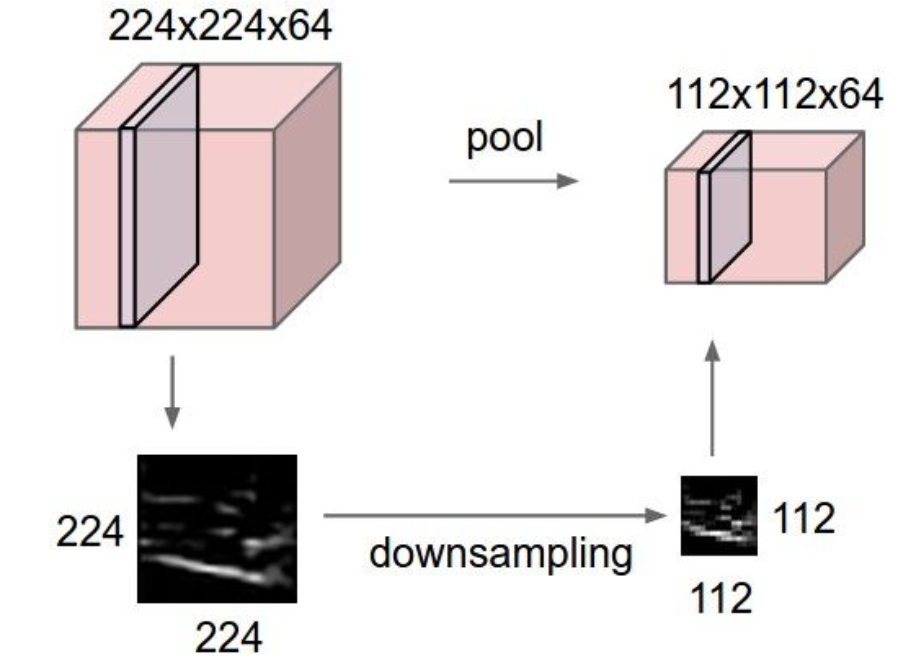
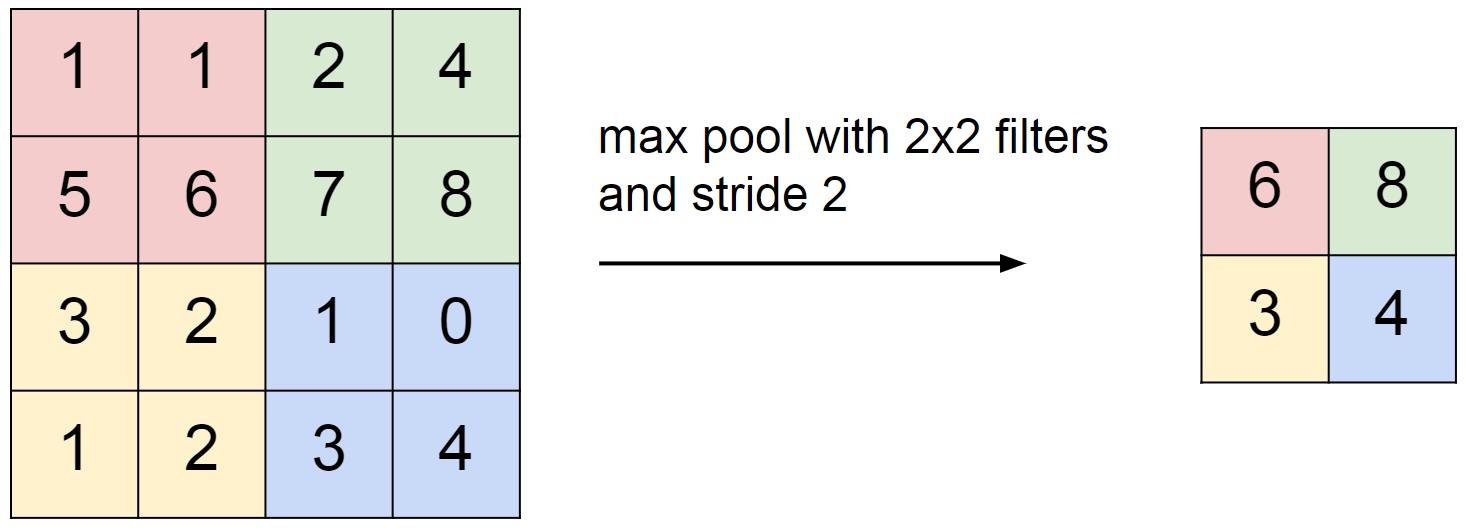
用的比较多的是 max pooling,就是取四个元素中最大的那个当作最终输出(如下图),除此之外还有其他的池化方法如 average pooling ,L2-norm pooling ,但在实际中还是 max pooling 表现得效果最好。一般池化层就紧接在卷积层的后面,降低 output 的维度,减少计算量
然而很多人都不喜欢池化层的操作,认为我们应该放弃池化层,追求简单性:全卷积网络!想着仅由重复的卷积层构成卷积神经网络的结构。为了减少特征大小,我们可以加大卷积模板的 stride ,并且这种设想在一些模型上已经表现出很好的效果,例如 GAN ,因此,未来的趋势可能是用越来越少的池化层甚至是不用了!
归一化层(normalization layer)
没什么卵用,只是记一下
全连接层(fully-connected layer)
全连接层中的神经元与前一层中的所有激活神经元都有完全的连接,就像在常规神经网络中看到的那样。因此,它们的激活可以通过之前的 WTx + b 来计算。
卷积层的输出转到全连接层就是通过用相同 Size 的卷积核模板与其相卷积,卷积之后就是全连接层的一个神经元了,全连接层有多少个神经元就要用多少个这样的卷积核卷积,所以全连接层的参数量巨大。
全连接之前的层负责找到图片的特征,全连接层负责将这些特征整合重组,因为空间结构特性被忽略了,所以全连接层不适合用于在方位上找 Pattern 的任务,比如 segmentation。
summary
一般卷积神经网络的结构都是像下面这样,但现在也有些网络不按这个套路出牌,总之,把这个模型搞懂的话简单入个门还是 OK 的,要知道每一层的作用是干啥的
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
然后下面就是一些注意事项,神经网络讲道理得多用才能在实际中记住并理解这些概念,不然的话,过段时间就会忘记了233333
- 输入层的尺寸应该要可以被 2 整除很多次,如 32, 64 ,96 等等
- 池化层应该设置成大小 2 x 2 ,使用步长为 2 的滑动窗
- 选择很多个小的卷积模板而不是一个很大的模板
- 选择 ImageNet 上表现最好的网络应用到你的项目中,不要想着造轮子
- 下载经过预训练的模型微调,甚至可以不用从头训练模型