preface
上节课讲到了损失函数,神经网络的目的就是让最终的损失 loss 尽可能小,因此不止损失函数,设计好一个优化器也是很必要的。
梯度
如果想要让 loss 减少得最快,我们就要顺着 loss 的梯度,因为梯度是函数值改变得最快的地方,二维平面计算梯度其实就是计算导数,多维平面计算导数就是求函数的偏导数
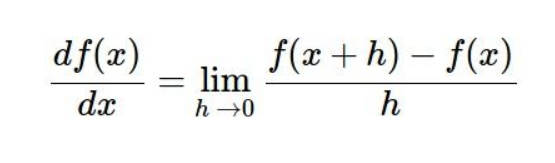
看看下面这张图,给出了已知的一个 W 权重向量,并且已知当前的 loss ,我们来想想梯度 dW 该怎么计算呢

首先让 W 的第一位维度增加一个很小的量,然后重新计算 loss ,这时可以看到 loss 减小了,然后我们用上面的公式,求解得到第一维的导数,以此类推,一直进行下去,将所有维度的导数都求完,得到的i向量 dW 就是梯度

但是这种方法在实际代码中是不可能会去用的,第一点,它非常慢,并且随着维度的增加,每计算一次梯度就得循环 W 所有的维度,相当于时间复杂度是 O(n) ,第二点,这样计算出来的结果也是近似的,并不是很准确。所以我们要尝试另一种更好的方法,那就是牛顿爷爷提出来的微积分,我们叫他解析梯度(Analytic gradient)
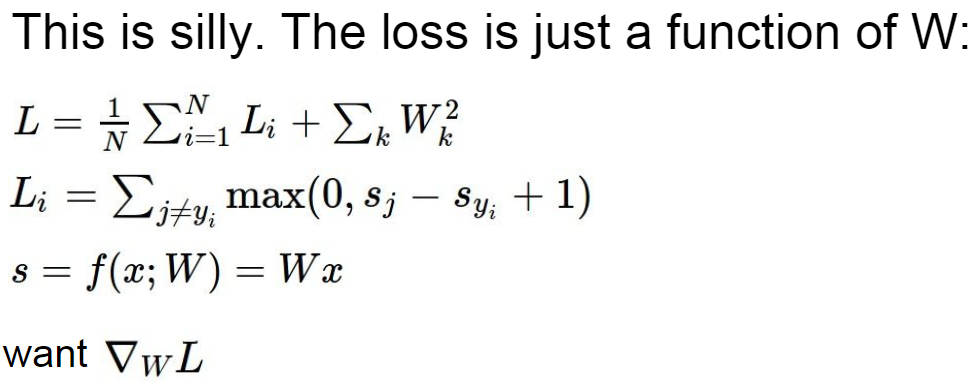
数字梯度(手动求导)的特点是慢,不准确,但是容易写,解析梯度的特点是精确,快速,但是容易出错。总结一下就是,我们在实际中会选择用后面的方法,但是可以用上面的求导数的方法来验证求得梯度的正确性或者用来 debug ,这是梯度检查的流程(gradient check)
梯度下降
神经网络最终的目的就是让 loss 尽可能小,所以我们要不断地更新参数 W 的值,将他训练成最优的参数,上面介绍了梯度的概念,梯度下降的概念也就很好理解了,就是下面这个公式

每一次 W 权重向量都会被更新,其中 step_size 是步长,就相当于人在山坡上往山下走每一次走多少路程,这是一个超参数,我们得在训练之前人为设定一个值
SGD 随机梯度下降
上面是说当我们的特征维度十分大的时候,我们就不能直接去计算内一个维度的导数了,通过微积分计算才有效率,这里讨论的是当我们的样本数十分大的时候,直接导入全部数据集计算的话会使得计算成本非常高,且计算量十分大,所以这里引出了 mini-batch 的概念,以局部代替总体,每次取 32,64 或者 128 个样本进去训练得出一个梯度,然后更新 W 的值,这就是 SGD(Stochastic Gradient Descent) 随机梯度下降的思想
