preface
之前介绍了 KNN 和线性分类器,这次终于上到神经网络了,这一节举了很多例子来说明神经网络的数学推导和反向传播的公式,如果忘记的话可以再回去看看
Neural Networks
在这之前,我们的分类器用的都是一个线性函数 f = Wx + b ,然而在神经网络这里,表达式也是差不多的,他稍微变化了一个形式,f = W2max(0, W1x) ,这里是一个两层的神经网络,其中的 max(0, W1x) 就是第一层神经网络的输出,因此多层神经网络的公式也就是不断地进行上面的操作
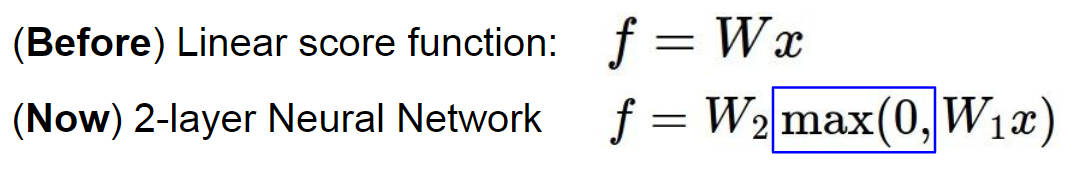
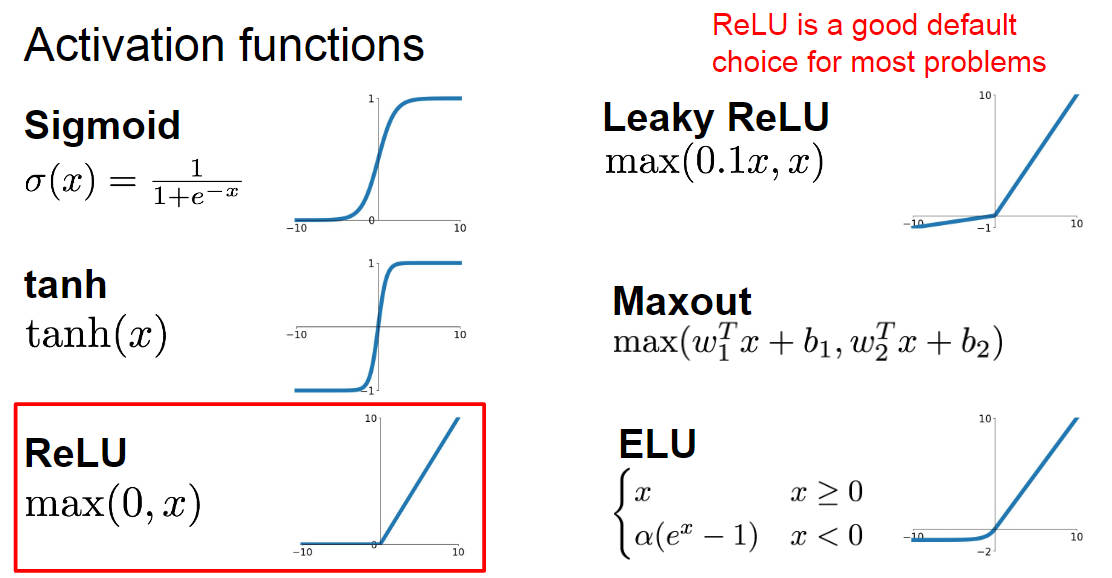
设想一下,要是我们不用后面的 max(0, W1x) 而是用 W1x 的话,公式就变成了 f = W2W1x ,这又是一个线性的分类器了,所以不能这样子,神经网络是个非线性的分类器。而 max(0, W1x) 这玩意被叫做激活函数(activation function),就是选择哪些神经元可以被激活,造成一种非线性的效果,激活函数的种类有很多种,其中 ReLU(Rectified Linear Unit) 是被用的最多的,如果不知道该用哪个激活函数的话就用 ReLU 吧
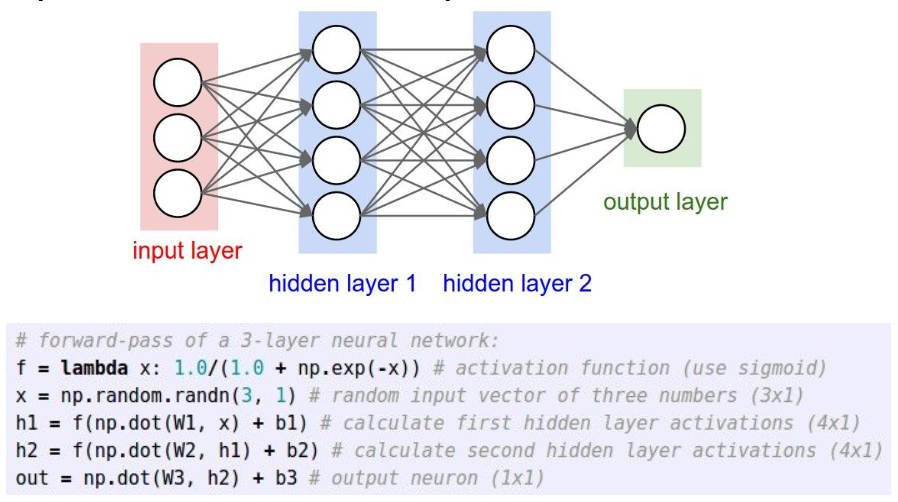
然后下面是一个三层神经网络的结构和代码表述(基础知识就不讲太细了)
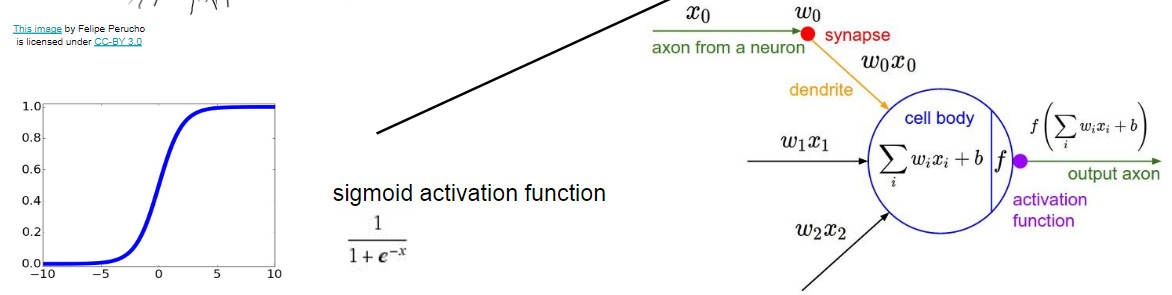
然后这是一个单独的神经元的长相,他长这样,就用输入的样本和每一个神经元的点积之和加上偏置,最后再通过一个激活函数进行输出
How to compute gradients
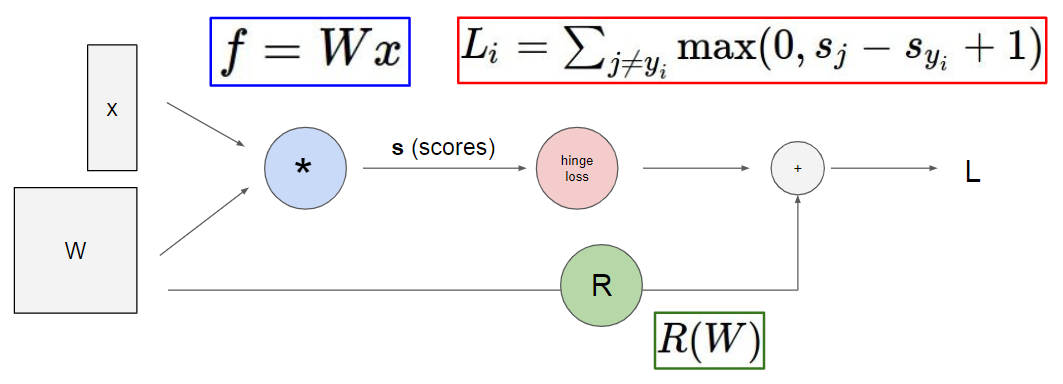
下面说说怎么样去计算神经网络的梯度,还是跟线性分类器那里一样按部就班来整一套,先给出一个 score function ,再给出一个 loss function ,其中 loss function 又包括了预测错误的损失和正则化的损失,不过再线性分类器中只有一个 W 的正则化损失,神经网络中每个神经元都包含了一个 W ,因此在计算正则化损失的时候得累加起来,然后用这个损失函数对 W 进行求偏导,然后就可以学习 W 这个参数
计算梯度的话,首先想到的可能就是手动推导,不过这样子非常 silly ,需要计算大量的矩阵运算,并且如果将损失函数由 SVM loss function 换成 softmax 的话又得重新运算一遍,最致命的问题,现在的网络模型可以变得很大,因此用这种方法计算梯度几乎是不行的。所以,另外一种更好的方法就是画出神经网络的计算流图,然后通过反向传播求得梯度
Backpropagation
虽然已经知道反向传播是个啥东西了,但还是用一个简单的例子来回顾一下,随便设几个常数
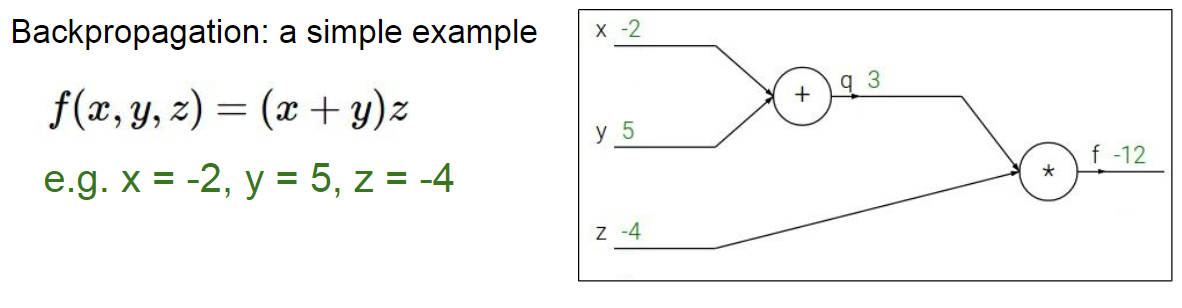
通过链式法则就可以求得最终的 f 对各个参数节点的偏导数

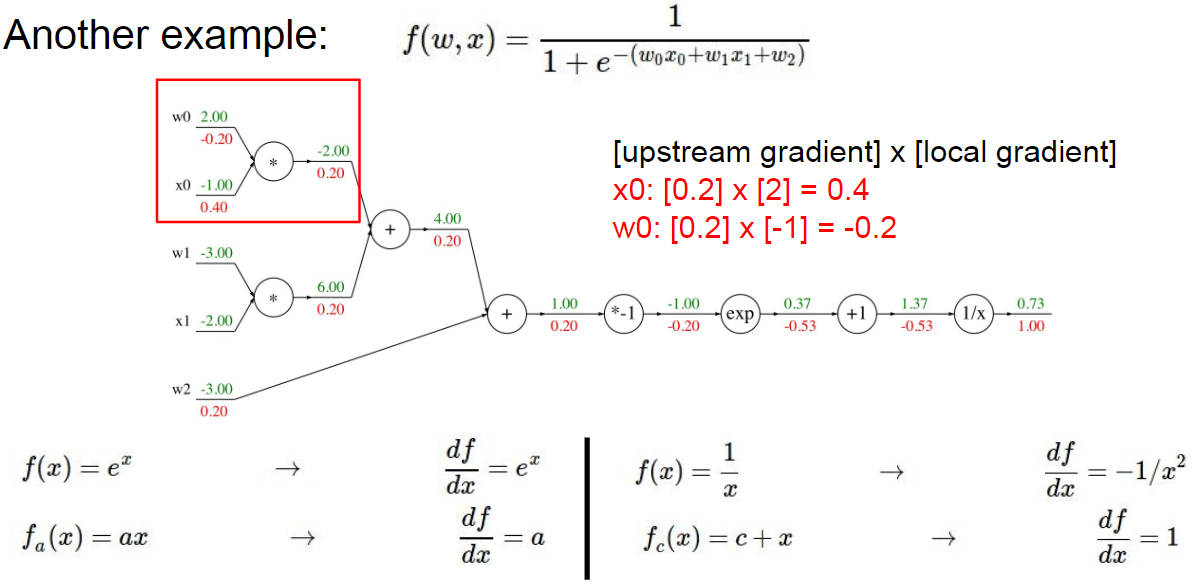
这里有给出一个复杂点的反向传播的例子,就是不断地用梯度相乘,不明白的可以再去看看对应的 PPT ,里卖弄讲解得非常详细
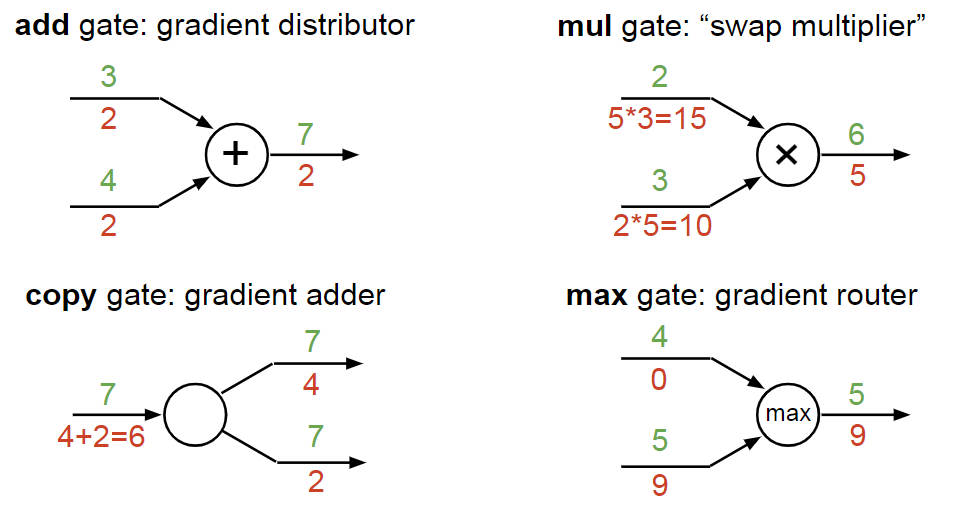
并且给出了常见的计算流图的反向传播的值的计算方法如下图(add, mul, copy, max)
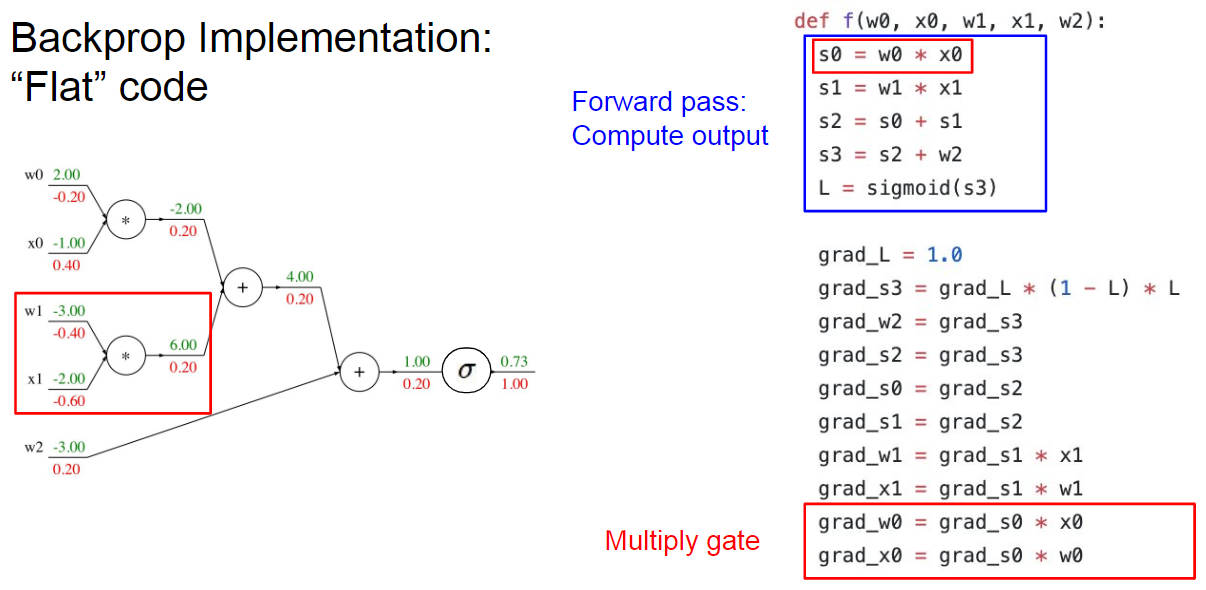
并且还将正向传播和反向传播的代码给写出来配合计算流图讲解,印象更加深刻,总之就是求偏导加上链式法则那一套咯
Backprop with vector-valued functions
上面讲的这些都是 Scalar 实数的求反向传播方法,要是各节点是个向量的话其实也是一样的,方法还是那样,只不过要注意的是求出来的导数的维度要和之前的向量的维度保持一致,不然就会出错,所以向量这里的话没有什么公式,一般是在纸上写一下各向量的维度信息然后进行推导一下代码应该怎样写
# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)
# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)
提示:使用尺寸分析! 请注意,您无需记住dW和dX的表达式,因为它们很容易根据尺寸进行推导。 例如,我们知道权重dW的梯度在计算后必须与W大小相同,并且它必须取决于X和dD的矩阵相乘(当X,W均为单数时就是这种情况) 而不是矩阵)。 始终只有一种方法可以实现这一目标,从而确定尺寸。 例如,X的大小为[10 x 3],dD的大小为[5 x 3],因此,如果我们希望dW且W的形状为[5 x 10],则实现此目的的唯一方法是dD.dot( XT),如上所示。
不过 PPT 里关于向量反向传播倒是扯得很复杂,甚至还提到了雅可比矩阵,后面看了一下下一篇文章才发现没有这么恐怖,也就是跟 Scalar 是一样的原理