preface
上节课讲的 KNN 效率很低,并不能满足大多数情况,主要体现在
- 分类器要记住所有样本的特征,但是今天的样本量可以达到几个 GB ,而且维度也会是以千万计。
- 要将测试集与所有的训练集进行比较,效率十分慢。
因此,用线性分类器这种方法来满足大多数情况下的分类,因为他只需要训练 W 和 b 参数,一旦训练好了,就可以把训练集给扔了,并且也不用与每一个训练集进行比较,只要做一些简单的矩阵相乘相加就行。
score function
线性分类器通过设计 Score function 和 Loss function 来实现分类, 函数原型如下
f(xi, W, b) = Wxi + b
-
xi 是输入样本的所有特征,假设输入是一个
4*4*3的样本,xi 就是他们展开的一个48*1的列向量 -
W 是权重(Weight),是一个
C*D的向量,C 是分类器最终输出的类型的个数,D 是一个样本中的特征数量,其实 W 就相当于是用 C 张图片去和输入的图片进行内积操作,选出得分(Score)最大的一个类别,最终分类的结果就是这个类。W 的每一排都相当于是一张模板图片展开,如下图给出了 CIFAR-10 的一个权重图,且 W 是在训练的过程中不断更新的,因为要确保这些参数能适应所有的训练集。
-
b 是偏置,也是我们需要训练的参数,相当于一次函数的截距,在线性分类器中相当于平移分隔面,而改变 W 的作用相当于是旋转了分隔面。

-
虽然 W 和 b 表示的是不同的意义,但是我们很多情况下都是将他们两个放在一起的,将 W 和 b 组成一个增广矩阵,这样的话,xi 就多了一个维度,只需要在最后增加一个
1,内积的结果就跟之前一毛一样了,这样子的好处就是我们只需要训练一个矩阵,而不用训练两个矩阵。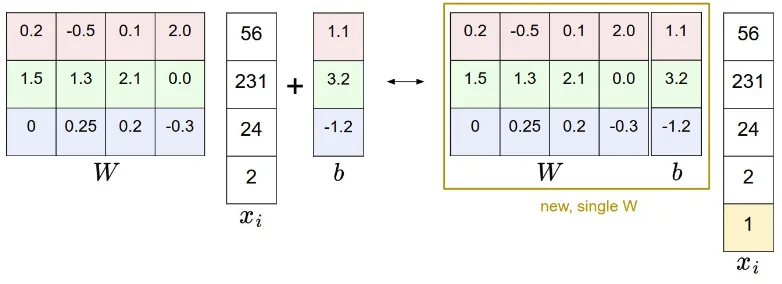
对图像而言,每一个像素都是一个特征,特征值在 [0,255] 之间,但是我们通常不这样做,通常要将特征值归一化(normalization),一种可能的做法是求出训练集中间的一张图片,然后让所有的图片与这张图片相减,得到的特征值大约在 [-127, 127] 间,更加普遍的做法就是让特征值保持在 [-1, 1] 之间。

假设我们输入一张猫的照片,分类器却跟我们说这是一条狗,那我们就会觉得这个分类器很垃圾,也就是说,W 训练得很垃圾,所以我们要用一些手段来不断地提高 W ,这就要用到 Loss function ,也叫 Cost function ,通俗点说就是:
输入一张猫片
分类器:狗 我:什么辣鸡,继续训练
分类器:还是狗 我:辣鸡,再去训练
分类器:猫 我:牛逼!
loss function
SVM loss
Loss function 的种类有很多,其中一种是 Multiclass SVM loss ,公式如下(其中 s 是 Score 的缩写):
Li = ∑j≠yi max(0, sj − syi + Δ)
Li = ∑j≠yi max(0, wTjxi − wTyixi + Δ) //推广到向量
SVM loss 大概的原理就是它有一个超参数 delta ,相当于一个 margin 吧,SVM 想让正确类别的分数至少比错误类别的分数高 delta ,如果分类之后错误的类的 Score 与正确类别的 Score 的差值在 delta 范围内的话就会产生 Loss ,否则 Loss 就是 0 ,也就是说其他类的得分比正确类的得分少很多。下图很好的解释了这个观点

但是上述的 Loss function 有个 bug, 那就是能让输出结果正确的 W 不止一个,因为线性分类器只需要做矩阵相乘就能够得到各个类别的 Score , W 乘以一个系数 λ 之后分类结果依然不变,但是 W 乘以一个系数 λ 后 Loss function 的值会改变,原本两个 Score 相减之后只有 10 ,乘以 2 之后差就变成了 20 ,如果 delta 设置的是 15 那么就会产生 Loss
为了消除这种歧义,引入了 正则化 Regularization 这个概念,我们要做的就是在上述的 Loss function 中加上正则化惩罚 Regularization Penalty , 这里用 R(W) 来表示. 最普遍的正则化惩罚函数就是 L2 范数 ,也就是对 W 的每一个元素都求平方再相加, 公式如下:
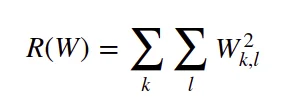
正则化的目的是防止模型在训练集上表现得太好,防止过拟合
注意到我们的正则化惩罚函数只是对 W 进行操作, 并没有对数据进行改动, 因此整一个 Loss function 应该包含两部分, 一部分是 data loss , 也就是所有数据样本的 Loss 的平均值, 再加上正则化惩罚, 公式表达如下:
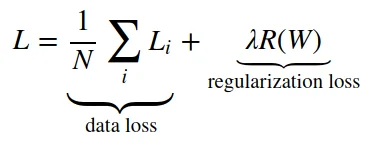
将公式展开得更具体点就是下面这个 Loss function , 其中 N 就是整个样本的数量, λ 也是一个超参数, 这个值一般是通过交叉验证来确定的. 当然, 老师讲到,在划分训练集的时候就得把标签弄正确,这有助于降低 loss.

Additionally, making good predictions on the training set is equivalent to minimizing the loss.
关于上述 delta 的选择方案: 纠结 delta 的具体值是没有意义的,因为 W 可以变大或变小,唯一的权衡因素是我们希望 W 怎样增长(在正则化系数 λ 的作用下)
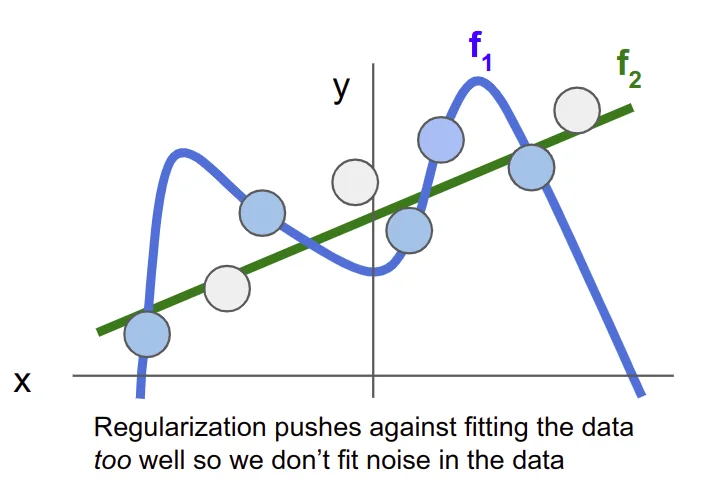
正则化:防止模型过拟合(在训练集上表现太好),简化模型(权重),使其在测试集上也能表现很好
Softmax loss
SVM 是常见的一种分类器,还有一种常见的就是 Softmax 了,记得之前在 Logistic regression 二分类问题中,我们可以使用 sigmoid 函数将输入 Wx + b 映射到 (0, 1) 区间中,从而得到属于某个类别的概率。将这个问题进行泛化,推广到多分类问题中,我们可以使用 softmax 函数,对输出的值归一化为概率值。
先来看看 softmax 函数的公式,就像下面这样,假设进入 softmax 之前,全连接层输出了样本的类别数,一共 C 个,因此有 C 个类别,用 a1, a2 , a3 …… ac 表示,因此,对于每个样本,它属于类别 i 的概率为:

公式的上面是 e 对当前输出的指数次方,下面是所有类别输出的指数之和,因此,很容易理解这是在求概率,函数相加之和(y1, y2, y3 ,……yc)为 1
然后 softmax loss 就用指数的形式来表示,像下面这样,这是 softmax 的 data loss 部分:

这个公式倒是好理解,不过课件中又有涉及到交叉熵的概念,交叉熵就等以后学到了再来讲吧,暂时不用用到
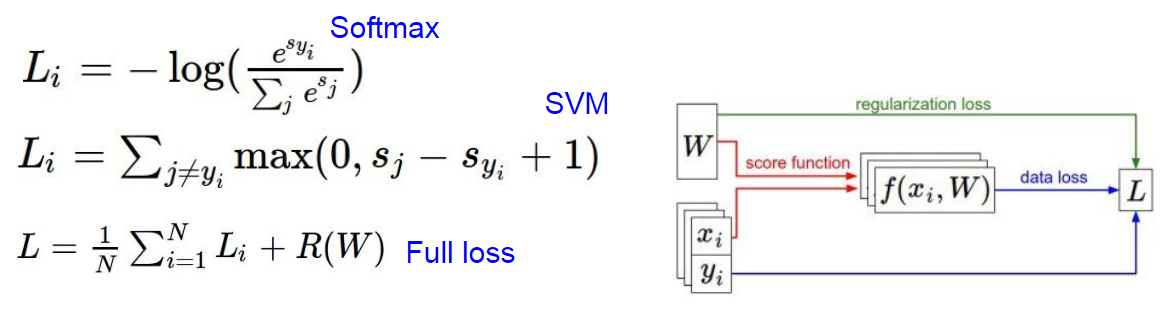
下面给出 softmax loss 和 svm loss 的对比图,可见 svm 就是用上面提到的 max 策略来计算 loss ,而 softmax 则是将输出进行指数操作,再归一化求得每一个类别的概率,最后用上面的公式来计算 loss ,这种方式可以将类别的概率(置信度)直观地呈现出来,但注意,softmax loss 得到 loss 的数字和 SVM loss 得到的数字没有可比性,只能在同一个分类器中进行比较
SVM 想要正确类别的 score 尽量高,softmax 想要正确类别的对数概率尽量高

但是 softmax 的概率也是相对来说的,因为概率的大小会受到正则化强度 λ 的影响,我们在之前 SVM 那里也说过了,权重矩阵并不是唯一的,随便乘以一个系数之后的分类结果依然不变,但是得出的概率就会变,下面的例子就说明了这一点:
假设全连接层输出三个类的分数是 [1, -2, 0] ,softmax 函数将作如下计算
[1,−2,0]→[e1,e−2,e0]=[2.71,0.14,1]→[0.7,0.04,0.26]
如果 W 被正则化惩罚得更多,W 就会 更小,假设现在 W 变成了 [0.5, -1, 0] ,那么新的计算如下
[0.5,−1,0]→[e0.5,e−1,e0]=[1.65,0.37,1]→[0.55,0.12,0.33]
虽然第一个类别的概率依然是最大的,但是就没有那么明显,概率依然是可信的,但是概率之间的差值从技术上是不可解释的。在实际中,SVM 和 softmax 的差别并不是很大,但是有人就他们的性能会有不同的看法,其实适合自己就好了。
summary
- 定义了线性方程 score function 将图像像素转化成各类别的 score
- 线性分类器使通过训练 W 和 b 起作用的,不用储存图像信息,比 KNN 高效很多
- 通过增广矩阵将 W 和 b 放在一个矩阵中就只用训练一个矩阵,不用训练两个
- 定义损失函数 loss function (介绍了两种在线性分类器上常使用的 loss :SVM 和 softmax) 来评估这些参数得出的结果有多贴近样本本身的类别,损失函数的定义是:对训练数据做出良好预测就等同于损失很小
reference
https://zhuanlan.zhihu.com/p/27223959